Что такое сложные проценты и как они влияют на доход от вкладов и инвестиций

Простой и сложный, в чем отличие

В математике один процент – одна сотая часть числа. Говоря о банковском проценте, обычно подразумевают сумму денег, начисленную по определенным правилам и скопившуюся к конкретному сроку.

Все условия начисления процентов обязательно указываются в договоре между сторонами. Имеют значение такие факторы:

• размер годовой процентной ставки,
• капитализация процентов,
• срок договора,
• порядок выплаты процентов.

Кроме размера ставки, т.е количества начисленных за год процентов, на конечную сумму существенно влияет наличие или отсутствие по условиям договора капитализации процентов.

Это приводит к тому, что один и тот же процент, начисленный в первый период, всегда меньше, чем в последующий – ведь база для исчисления процента вырастает со временем.Такой процент называется сложным процентом.

Во вкладах и кредитах, где база для начисления процента не меняется со временем, всегда остается равной первоначальной сумме, расчет производится по формуле простых процентов.

Сложные проценты в EXCEL. Постоянная ставка

Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

В файле примера приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов читайте здесь .

Использование офисных программ для работы со сложными процентами

Любой офисный пакет, а именно его табличный процессор, предоставляет множество функций для денежных расчетов: от самых простых и до самых сложных. Достаточно просто выбрать нужную (или несколько) для составления своих формул. Если использовать возможность программировать на VBA в Excel, то можно получать более быстрые результаты при расчетах. Когда рассчитывается сложная процентная ставка, формула может быть простейшей рекурсией без всяких степеней и логарифмов. Все сделает цикл с параметром в число периодов начисления. При необходимости можно легко добавить сумму периодического инвестирования, не ломая голову над выводом или поиском формул.

В примере, показанном ниже, используется, правда, не MS Excel, а LibreOffice Calc, – близнец Экселя для UNIX-подобных операционных систем. Но это, в принципе, ничего совершенно не меняет. Код макроса для OOBasic хоть и отличается от экселевского, но только в технических деталях.

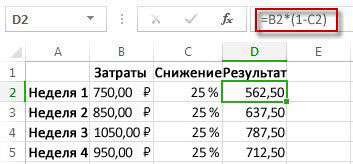
В примере на рисунке выше мы рассчитываем как сложные, так и простые проценты по вкладу 8,6% годовых. Проценты начисляются каждый год, а вклад рассчитан на 18 лет вперед. Начальный взнос 25 тыс. рублей мы (условно) делаем 1 января 2017 года. Если мы хотим сравнить графики для этих результатов, что, конечно, более наглядно, то добро пожаловать на следующий лист, в который этот самый график очень легко вставить.

Пример показывает, что за прошедший срок составные проценты вдвое превышают простые.

Еще один пример. Можно легко переделать нашу модель и снять ограничение на ежегодную капитализацию. Тогда мы можем решить еще одну задачу. Предположим, что мы открыли центовый счет на бирже Forex и хотим поучаствовать в торговле валютами. Считая, что мы умеем, добросовестно работая с информацией, расти на 10% в день (что, может быть, слегка самонадеянно, но бог с ним), посмотрим, что получится из депозита в одну тысячу рублей, за месяц, т.е. 22 рабочих дня. Для этого чуть изменим формулу для нашего постоянного множителя:

Теперь мы избавились от (довольно искусственного) ограничения на ежегодный пересчет процентов. И получаем такую картину:

А на графике можем видеть рост и разницу между составными и обычными процентами:

И здесь видна разница между простыми и составными процентами.

Что такое сложный процент в инвестициях простыми словами

Знание механизма расчета по депозиту позволяет вкладчикам составить прогноз дохода. Этот расчет доступен при заключении соглашений, выполнении транзакций, перед начислением вознаграждения и капитализацией прибыли.

Банки пользуются простыми и сложными формулами.

При этом применяется фиксированная ставка, которая закрепляется договором при размещении депозита, может регулироваться в случаях:

• автоматической пролонгации договора;
• досрочного закрытия.

Плавающий тип может меняться на протяжении действия соглашения.

Изменение ставок в этом случае привязано к таким факторам:

• курсу валют;
• переводу депозита в другую категорию.

При расчете дохода учитывается ряд показателей:

• инвестиционная сумма;
• процентная ставка, ее тип;
• периодичность начислений;
• срок договора.

При использовании простой схемы расчета итог получается в результате таких математических действий. Начальная сумма умножается на годовую ставку и количество дней начисления вознаграждения и делится на количество дней по календарю и на 100.

Зачем инвестировать под сложный процент

При инвестировании денег рекомендуется выбрать оптимальный вариант, который позволит использовать преимущества сложных ставок. Вложению денег всегда предшествует планирование, анализ поставленной задачи. Капитализация прибыли от инвестирования на счет позволяет получить дополнительный доход.

Простой расчет

Эффективной ставкой считается номинальный процент, который начисляется на сумму с капитализацией. Рассчитать доход можно в программе Excel. Для этого следует ввести исходные данные, формулы на базовый депозит, сумму с капитализацией. Действия выполняются автоматически, поэтому для получения корректного результата рекомендуется внимательно ввести информацию.

Формула

Плата за пользование средствами финансовым учреждением начисляется ежемесячно. Если вкладчик не будет снимать эти средства со счета, то они дополнят сумму основного депозита.

Формула сложного процента записывается: S=X*(1+%)n, где

• S — конечная сумма;
• X — начальный вклад;
• % — годовая ставка;
• n — количество периодов.

В результате прибыль добавляется к сумме и дает доход. Сложный расчет может действовать при открытии .

Выбирая программное предложение банка, нужно ориентироваться на итоговый доход в денежном выражении, который получится при размещении средств.

Простой расчет сложных процентов

Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль — 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.

Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.

Формула простых процентов.

Она используется тогда, когда начисляемый доход присоединяется к основному телу депозита в конце его срока или не присоединяется и выводится на текущий счет или пластиковую карточку. Этот порядок расчета стоит учесть, когда размещается солидная сумма на длительный срок. Обычно в данном случае банки применяют варианты размещения без капитализации, что понижает общую выгоду вкладчика.

Формула простого %:
Сумма % — это  доход, полученный через i-ый промежуток времени.

Р – изначальный объем вложений.

i – депозитная годовая ставка.

t – срок вложения.

T – число дней в году.

Рассмотрим пример: разместим 100 000 рублей на полгода под 12%. Рассчитаем полученный доход:

Таким образом, через полгода со счета можно будет снять 105 950,68 руб.

Что такое сложные проценты

Те, кто хоть раз размещал капитал, независимо от выбранного инструмента (депозит, облигации или акции), наверняка, слышал о сложных процентах. Исходя из названия понятно, что это именно доходность капитала. Но почему же она является сложной и как ее считать?

Если говорить простыми словами, проценты, полученные от капитала, инвестор не расходует на собственные нужды, а вкладывает их в тот же инструмент. В результате этого на следующую дату выплаты дохода они будут начисляться не только на сумму основного капитала, но и на проценты, вложенные в прошлом периоде. Этот маневр также называется реинвестированием, а в банковской среде он более известен как капитализация процентов.

Подобная политика реинвестирования процентов позволяет с каждым годом увеличивать не только сумму основного капитала, но и значительно повысить его доходность. При этом, чем больше срок вложения, тем сильнее заметен положительный эффект, если сравнивать его с расчетом простых процентов. Так, даже относительно небольшую сумму вложений можно увеличить в разы уже через 4-5 лет, а спустя более долгий период времени можно сколотить неплохой капитал. Конечно, многое зависит и от выбранного инструмента. Но, тем не менее, сложные проценты всегда дают положительный эффект.

Преимущества инвестирования с применением сложных процентов:

• Накопительный эффект. При инвестировании с капитализацией на конец периода инвестор будет иметь только первоначальную сумму основного капитала и начисленные за последний период проценты. Используя политику сложных процентов, инвестор на конец периода будет иметь первоначальную сумму со всеми начисленными за весь период процентами.
• Ежегодное повышение суммы доходности, даже если основная ставка инструмента не меняется. За счет увеличения суммы основного капитала на начисленные в прошлом периоде проценты, увеличивается и сумма для исчисления доходности в текущем промежутке времени.
• Возможность увеличения первоначального капитала без дополнительных вложений.

Вручную

Для этого нам понадобится вот эта формула:

• ФК – это наш финальный капитал или конечный результат. В общем, та сумма, которую мы получим на финише с учетом накопительного эффекта сложных процентов. Кстати, очень настраивает на регулярные инвестиции! Полезно своими глазами увидеть, в какие суммы превращаются даже небольшие вложения через 5,10 или 20 лет
• Ко – это начальный капитал, который мы инвестируем на длительный срок по принципу «вложили – и не трогаем»
• R – годовая процентная ставка в долях (например, 12% годовых будут выглядеть как 0,12)
• m – период реинвестирования в месяцах. Проще говоря, как часто будут начисляться проценты по вкладу и плюсоваться к общей сумме. Если ставка по банковскому вкладу начисляется каждый месяц, то m будет равно 1, если ежеквартально – то 3, если раз в году – то 12
• n – количество периодов реинвестирования. Например, если проценты реинвестируются раз в месяц, то за год получается 12 периодов реинвестирования, а за пять лет n будет равно 60

Теперь осталось сформировать простенькую табличку в Excel: из пяти строчек и двух столбцов.

• Строчка №1 – начальный капитал (Ко)
• Строчка №2 – годовая процентная ставка ( R )
• Строчка №3 – период реинвестирования (m)
• Строчка №4 – количество периодов (n)
• Строчка №5 — финальный размер капитала (ФК)

Первые четыре строчки мы заполняем вручную. В каждой из них формат будет «общим», и только годовую процентную ставку нужно прописывать в формате «процентный».

А дальше в ячейке с финальным капиталом забиваем формулу (по номерам строчек): =№1*(1+(№2*№3/12))^№4. На всякий случай, значок «^» в Excel находится так: «Вставка» — «Символ» — «^» — «Вставить», или с помощью комбинации клавиш «Shift+6» в английской раскладке.

Все, простейшая таблица в Excel готова! Теперь можно «играться» с размером начального капитала, годовой ставкой и количеством периодов. И видеть, как растет (или уменьшается) величина финального капитала.

Формулы расчета

Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.

Простой процент

Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.

Формула расчета:

S_N = S_П * (1 + % ст * N), где

• S_N – сумма в конце периода N;
• S_П – первоначальная сумма капитала;
• % ст – процентная ставка (доход);
• N – расчетный период.

Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.

В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.

В этом случае формула примет вид:

S_N = S_П * (1 + % ст * Д / 365), где

Д – количество полных дней нахождения денег на депозите.

Например:

1. Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
2. На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
3. На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.

Сложный процент с начислением дохода 1 раз в год

По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:

S_N = S_П * (1 + % ст)N

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.

Сложный процент с начислением дохода чаще, чем 1 раз в год

Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:

S_N = S_N * (1 + % ст / К)N*К, где

К – частота начисления дохода (12, 4 или 2 раза в год).

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.

Сложные проценты и использование других калькуляторов для их расчёта

В Интернете предлагается ряд бесплатных приложений по расчёту дивидендов. Многие портативные калькуляторы также могут выполнять эти задачи.

Бесплатный калькулятор капитализации предлагается через финансовые сайты. Он прост в использовании, предлагает выбор смешанных частот от ежедневного до ежегодного. Включает в себя возможность выбора непрерывной компоновки, позволяет вводить фактические даты начала и окончания календаря. После ввода необходимых расчетных данных в результатах отображаются:

• полученные суммы;
• будущая стоимость;
• годовой процентный доход (представляет собой показатель, включающий начисления процентов и ежедневные надбавки);

Различные финансовые сайты предлагают бесплатный онлайн-калькулятор сложных дивидендов. Это приложение довольно простое в использовании. Позволяет вводить ежемесячные дополнительные депозиты к основной сумме. Это полезно для расчета прибыли, когда вносятся дополнительные ежемесячные сбережения. Иногда рассчитывать сложные надбавки помогают финансовые специалисты, работники банков и других учреждений.

Частота составления

Интерес клиента может составлять любой график частоты, от ежедневного до ежегодного. Существуют стандартные схемы составления частот. Они обычно применяются к финансовым инструментам.

1. Для депозитных сертификатов. Типичные графики составления частот – ежедневные, ежемесячные или полугодовые.
2. Для счетов денежного рынка – также ежедневные.
3. Для ипотечных ссуд, ссуд на акции, личных ссуд для бизнеса или счетов кредитных карт наиболее часто применяемый составной график составляется ежемесячно.

Также могут быть различия во временных рамках. Тогда начисленные проценты фактически зачисляются на существующий баланс. Надбавки по счету могут насчитываться ежедневно, но зачисляются только ежемесячно. Когда суммы фактически начисляются или добавляются к существующему балансу, они начинают в сумме давать дополнительные проценты на счет.

Некоторые банки также предлагают то, что называется непрерывно сложным процентом. Он делает добавления к основной сумме в любой момент. В практических целях это не накапливает намного больше, чем ежедневные начисляемые надбавки. Исключением является случай, когда клиент не хочет вкладывать деньги и снимать их в тот же день. Более частое начисление дивидендов выгодно инвестору или кредитору. Для заемщика выгодна обратная ситуация.

Совокупный среднегодовой темп роста

Среднегодовой темп роста широко используется для расчета доходов за периоды времени для:

• акций;
• паевых инвестиционных фондов;
• инвестиционных портфелей;

Также он используется для определения нормы прибыли. Изучается, превысил ли управляющий взаимным фондом или портфельным управляющим рыночную норму прибыли за определенный период времени. Например, рыночный индекс обеспечил общую доходность в 10% за пятилетний период. Управляющий фондом генерировал только 9% годовой доходности за тот же период. В таком случае он уступил рынку.

Совокупный среднегодовой темп роста также может быть использован в других целях (для расчета ожидаемого темпа роста инвестиционных портфелей в течение длительных периодов времени). Это полезно для таких целей, как сбережения для выхода на пенсию.

Сложные проценты

Сложные проценты

РешитьСложная процентная ставка наращенияm=12m=4S=P·(1+im​)m·nсмешанным методомn

Современная стоимость Р величины S находится в случае сложной процентной ставки по формуле:
P=S(1+i)n​

Примеры задач на сложные проценты

1. Какой величины достигнет долг, равный P = 1 млн.руб., через n = 5 лет при росте по сложной ставке i = 15,5% годовых, если проценты начисляются раз в год, ежемесячно, поквартально и два раза в год?
   1) Сложные проценты начисляются раз в год:
   2) Сложные проценты начисляются два раза в год:
   S=1 000 000·(1+0,1552​)2·5 = 2 109 467,26 руб.
   3) Сложные проценты начисляются 4 раза в год (поквартально):
   S=1 000 000·(1+0,1554​)4·5 = 2 139 049,01 руб.
   4) Сложные проценты начисляются ежемесячно (12 раз в год):
   S=1 000 000·(1+0,15512​)12·5 = 2 159 847,20 руб.
2. Через n = 5 лет предприятию будет выплачена сумма S = 1 млн.руб. Определить ее современную стоимость при условии, что применяется ставка сложных процентов i = 10% годовых.
   P=S(1+i)n​
   P=1 000 000(1+0,1)5​ = 620 921,32 руб.
   Если проценты начислялись ежеквартально.
   P=S(1+im​)m·n​
   P=1 000 000(1+0,14​)4·5​ = 610 270,94 руб.
3. Определить современную стоимость S = 20 тыс.руб., которые должны быть выплачены через четыре года (n = 4). В течение этого периода на первоначальную сумму начислялись сложные проценты по i = 8 %годовых: а)ежегодно; б)ежеквартально.
   P=S(1+i)n​
   P=20 000(1+0,08)4​ = 14 568,92 руб.
   Если проценты начислялись ежеквартально.
   P=S(1+im​)m·n​
   P=20 000(1+0,084​)4·4​ = 14 570 руб.
4. За взятые в долг деньги под сложную процентную ставку i=35% годовых должник обязан уплатить кредитору 30 тыс. руб. 1 июля 1997 г. Какую сумму необходимо уплатить должнику, если он вернет долг: а) 1 января 1997 г.; б) 1 января 1998 г.; в) 1 июля 1999 г.?
   Количество дней в 1997 году: T=365.
   а) 1 января 1997 г.;
   Эта дата ранее 1 июля 1997 г., поэтому речь идет о поиске P (S=30000). Количество дней между 1 января 1997 г. и 1 июля 1997 г. составляет d=181 дн..
   б) 1 января 1998 г.;
   Эта дата позже 1 июля 1997 г., поэтому находим S (P=30000). d1=01.07.1997 и d2=01.01.1998.
   в) 1 июля 1999 г.Количество лет между 1 июля 1997 г. и 1 июля 1999 г. составляет n=2 года.
   S=P·(1+i)n=30000·(1+0.35)2 = 54 675 руб.

Дисконтирование

Дисконтирование – это процесс определения текущей стоимости денег, когда известна их будущая стоимость. Дисконтирование дохода применяется для оценки будущих денежных поступлений (прибыль, проценты, дивиденды) с позиции текущего момента.

Дисконтирование выполняется путём умножения будущих денежных потоков (потоков платежей) на коэффициент дисконтирования:

Экономический смысл дисконтирования (на примере)

Через 2 года Вам нужно будет 1 000 000 рублей, чтобы купить автомобиль. У Вас есть возможность положить деньги в банк под ставку 10%. Какой суммой денег нужно обладать сейчас, чтобы в будущем купить автомобиль?

Нам нужно будет 826 446,29 рублей, чтобы сейчас их инвестировать с доходность в 10% ежегодно  и через 2 года снять 1 000 000 рублей.

Проверим это:

826 446.29 * 1.1*1.1 = 1 000 000 рублей.

Что такое сложный процент

Сложным процентом называют процент, начисляемый на первоначальную сумму, позже прибавляемый к ней и далее начисляемый уже на новую общую сумму.

При этом ранее начисленный доход сохраняется. Так длится до конца расчетного периода. В условиях депозита – это так называемая капитализация процентов.

При ежемесячной капитализации сумма, начисленная в процентах, прибавляется к первоначальной сумме. Во второй месяц проценты начисляют уже на новую общую сумму.

И так повторяется каждый месяц, пока не закончится срок депозита. Если по условиям депозитного предложения счет можно пополнять, то сумма увеличится в разы.

При отсутствии капитализации, проценты начисляют только на сумму, находящуюся на счете.

Что еще почитать и посмотреть

Если вы читаете эту статью, потому что интересуетесь инвестициями, я вам очень рекомендую вот эти материалы:

1. Акция.
2. Облигация.
3. Контрольный пакет акций.
4. Общая статья про инвестиции.
5. Форекс.
6. Биржа.

Статьи я стараюсь писать простым и человекопонятным языком. Чтобы люди без экономического образования легко могли их понимать.

Еще я вам рекомендую два курса. Первый – «Финансовая грамотность» от онлайн-университета Скиллбокс. Этот курс в целом про деньги – про банковские вклады, кредиты, ведение бюджета.

Там поднимается очень много жизненных вопросов, которые, как мне кажется, помогут вам избежать серьезных проблем. Например, преподаватели объясняют, что делать, если нечем платить ипотеку, на что смотреть при выборе банковского вклада и пр.

Второй – «Личные финансы и инвестиции» от Нетологии. Здесь уже тема более заточена под инвестиции. Вы узнаете обо всех финансовых инструментах, в которые можно вкладывать деньги, о том, как определять риск в инвестициях и контролировать его, как правильно делать диверсификацию капиталовложений.

Я смотрел оба этих курса. Они проводятся так: вы смотрите видеоролики, а потом проходите тесты. Преподаватели всегда на связи и готовы ответить на любые вопросы.

Еще один хороший плюс – с преподавателями можно не терять связь даже после окончания курсов. Если в случае с финансовой грамотностью это будет не так актуально, то вот в курсе по инвестициям обратная связь будет очень кстати, когда начнете реально вкладывать деньги.

Из бесплатных материалов могу порекомендовать вам записи вебинаров от банка АкБарс. Вот одна такая запись, можно ее смотреть прямо отсюда.

И последнее – три книжки по инвестированию от проекта Город Инвесторов. Я даю материалы именно этого ресурса, потому что я сам их читаю, и потому что там проходил платные курсы Василий Блинов, который создал этот сайт. Так что ресурс надежный, мы лично это знаем.

1. Как стать финансово независимым через 1 год. Эта книга – о том, как применять советы знаменитого бизнес-тренера Роберта Кийосаки в России. Автор – практикующий инвестор.
2. 5 способов эффективно вложить 1000+ рублей. В книге делается обзор реальных примеров инвестирования маленьких денежных сумм, начиная от тысячи рублей. Автор дает по каждому примеру развернутый комментарий.
3. 6 шагов к финансовой безопасности. О том, как разными способами усовершенствовать свое финансовое положение. Как начать путь к финансовой свободе и достичь ее в максимально короткие сроки.

Пожалуй, всё.

Как выбрать лучшие условия?

Начисление простых процентов происходит в арифметической прогрессии, в то время как сложные проценты выдают прибыль в прогрессии геометрической.

Это не означает, что для успешного вложения всегда стоит останавливать свой выбор на предложении с капитализацией вклада.

С учетом срока действия депозитного договора, суммы вклада, и (что самое основное) периодичности начисления процентов, не всегда прибыль от капитализации будет больше, чем при заключении договора с одноразовой выплатой процентов в конце периода.

• При заключении договора на 3 месяца и периодичности капитализации в 6 месяцев, клиент заберет свой вклад раньше, чем произойдет начисление процентов. В этом случае оформление простого вклада будет иметь более логичный смысл.
• Также, если есть возможность выбора частоты начисления процентов (каждую неделю, месяц или три месяца), лучше выбрать капитализацию, где проценты будут приходить на счет в более короткие термины. Выбирая между периодичностью начислений в три месяца и один, примите решение в пользу последнего.
• При открытии краткосрочного вклада, клиентам банка нужно учесть, что на день закрытия депозита начисление процентов не происходит. Если вкладчик оформил договор на 2 недели и забирает средства на 14-й день, то начисление процентов будет произведено только за 13 дней.

В тексте депозитного договора буквально не говорится, будет происходить начисление простых или сложных процентов. Поэтому, исходя из условий договора, клиент сам должен понять, о чем идет речь.

Основное отличие:

• Если процент начисляется один раз по окончании срока действия депозита, расчет будет произведен по простой формуле.
• Если указана частота начисления процентов, вы имеете дело с капитализацией.

Самое выгодное для вкладчика:

• депозит с капитализацией,
• ежемесячное начисление процентов,
• возможность пополнения счета.

По таким вкладам, правда, у банков редко бывают высокие процентные ставки. Но здесь уже каждый клиент должен сам искать более выгодное решение.

Как получать сложный процент

Для этого вы при инвестировании денег должны сделать две вещи.

Уточнить условия инвестиций

Надо выяснить, как рассчитываются проценты – по простой или по сложной схеме. Например, в банке проценты чаще всего сложные, на картах с процентом на остаток – тоже.

Если в условиях будет указано, что процент простой – сложным вы его никак не сделаете. Увы.

Реинвестировать доход

Чтобы сложный процент делал вас богаче и богаче, вы должны реинвестировать свои деньги, то есть повторно их вкладывать. Или просто не выводить.

На банковском вкладе происходят как бы автоматические реинвестиции. Вот вы получили за первый год сто тысяч на свой миллион, не вывели их – на следующий год получите уже не сто, а сто десять тысяч. Сложный процент тут работает без вашего участия.

А вот если вы вкладываетесь, например, в акции, то сложный процент можно получить только через самостоятельное реинвестирование. Например, вы вложили миллион, акционерное общество выплатило вам 50 000 рублей дивидендами. Теперь вам надо эти 50 000 самостоятельно вложить в новые акции. Иначе сложный процент не заработает.

Заключение

Даже спустя сотни лет после открытия, сложные проценты не теряют своей популярности и значимости. Это мощный инструмент в финансовом мире для приумножения капитала. Не имеет значения являетесь вы крупным инвестором или просто держите депозитный счет в банке. Более важным будет ваше мастерство находить самые выгодные предложения.

Согласитесь, ведь куда лучше сделать вклад с меньшей процентной ставкой, но с возможностью капитализации доходов. Чем положить деньги с высокой ставкой, но без такого преимущества.

Алексей

Активно инвестирую в высокодоходные, перспективные направления. Делюсь опытом и рассказываю про актуальные варианты заработка.