Построение графиков функций

Как добавить линию на график

Иногда требуется обозначить на графике некоторые контрольные значения или коридор, например, среднее значение и сигму-окрестность.

Однажды, выступая на конференции с докладом «Как повысить качество управленческих решений» мне потребовалось проиллюстрировать разброс числа рекламаций в течение года (рис. 1).

Наряду со значениями (красные точки), я вывел на графике линию среднего значения (зеленая линия) и верхнюю границу диапазона, соответствующую отклонению 3s от среднего значения (синяя пунктирная линия):

Рис. 1. График со средним и границей

Скачать заметку в формате Word, примеры в формате Excel
Построение такого графика не должно вызвать затруднений. Рассмотрим лист «Коридор» Excel-файла:
Во второй колонке указаны значения средней дебиторской задолженности по месяцам, в третьей – среднее значение по году, вычисленное по формуле =СРЗНАЧ($B$2:$B$13), в четвертой – нижняя граница, соответствующая значениям на s меньше среднего =C2-СТАНДОТКЛОН($B$2:$B$13), в пятой – верхняя граница, соответствующая значениям на s больше среднего =C2+СТАНДОТКЛОН($B$2:$B$13).
Примечание

Чтобы отразить данные в миллионах рублей, я использовал специальный (пользовательский) формат:
Обратите внимание, что после # ##0,0 имеются два пробела.
Строим стандартный график:

Форматируем линии: убираем маркеры на опорных линиях, меняем цвет и тип линий, убираем линию на основных данных. Удаляем линии сетки, чтобы наши контрольные линии лучше выделялись. Добавляем релевантный заголовок нашему графику:

В принципе, график готов. Если ваш эстетический вкус ???? не удовлетворен тем, что контрольные линии не касаются границ области построения, можете добиться этого, потратив некоторое время.

1. Выделите одну из контрольных линий, например, линию среднего, и правой кнопкой мыши вызовите контекстное меню; выберите пункт «Формат ряда данных»:
2. Поставьте переключатель в положение «По вспомогательной оси»:
3. Повторите процедуру для линий, обозначающих верхний и нижний коридоры. Должно получиться следующее:
4. Перейдите на вкладку Макет и пройдите по меню Оси — Вспомогательная горизонтальная ось — Слева направо
5. Выделите вспомогательную горизонтальную ось и переключите «Положение оси» в позицию «по делениям»:
6. Диаграмма должна выглядеть так:

Выделите и удалите вспомогательную вертикальную ось. При этом контрольные линии расположатся в соответствии с основной вертикальной осью.

А вот горизонтальную вспомогательную ось удалить нельзя, так как настройки контрольных линий (вспомогательная горизонтальная ось в положении «по делениям») пропадут.

Поэтому нужно выделить горизонтальную вспомогательную ось и отключить основные деления и подписи оси:

Вот что у нас получилось:

Небольшое домашнее задание. Попробуйте сделать невидимой вспомогательную горизонтальную ось.

Полный пример решения онлайн

Лучшее спасибо — порекомендовать эту страницу

Провести полное исследование и построить график функции
$$
y(x)=\frac{x^2+8}{1-x}.
$$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, \quad \Rightarrow \quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-\infty; 1) \cup (1;+\infty).
$$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x \in (-\infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x \in (1; +\infty)$ функция $y\lt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):

Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

При $x \in (-\infty; -2), (4;+\infty)$ производная $y’ \lt 0$, поэтому функция убывает на данных промежутках.

При $x \in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.

При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x \in (-\infty; 1)$ выполняется $y» \gt 0$, то есть функция вогнутая, когда $x \in (1;+\infty)$ выполняется $y» \lt 0$, то есть функция выпуклая.

8) Исследуем поведение функции на бесконечности, то есть при .

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Построение графика функции f(x)

Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой

Рис. 6. Построение графика функции f(x)

Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=…., поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7

Рис. 7. Построение двух графиков функции

Построение графика

Для определения максимумов и минимумов функции, точек перегиба, промежуточных точек необходимо строить асимптоты. Для удобного обозначения фиксируются промежутки возрастания, убывания, выпуклость, вогнутость. Рассмотрим на рисунке, изображенном ниже.

Необходимо через отмеченные точки проводить линии графика, что позволит приблизить к асимптотам, следуя стрелочкам.

На этом заканчивается полное исследование функции. Встречаются случаи построения некоторых элементарных функций, для которых применяют геометрические преобразования.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

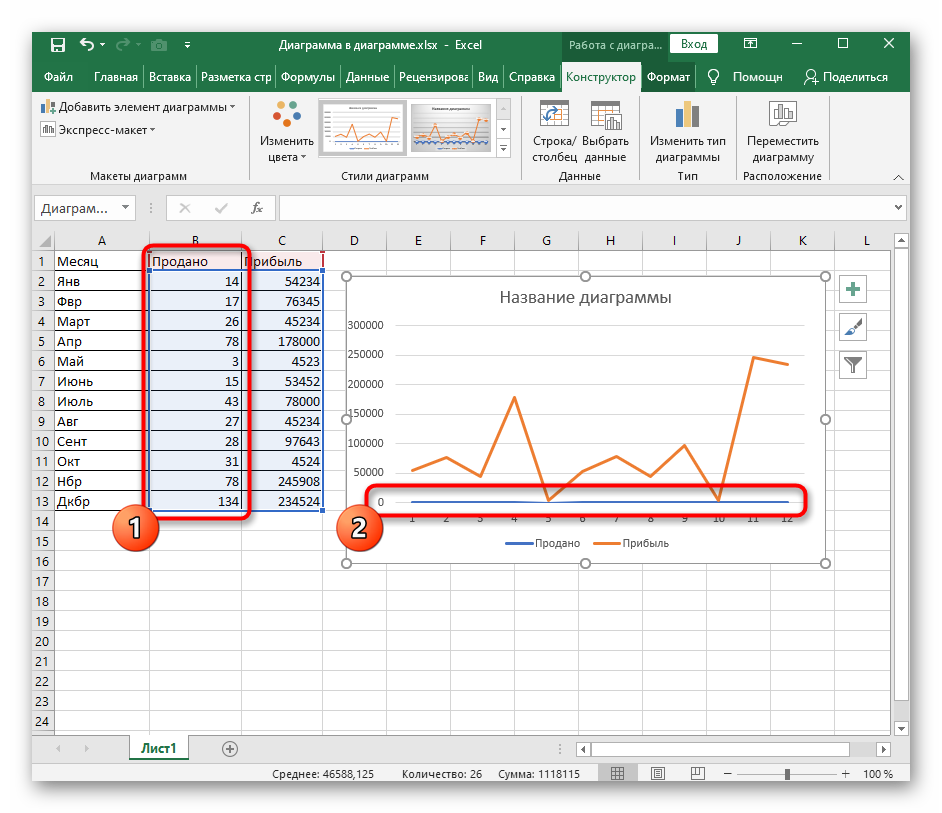
Особенности оформления графиков в Excel

Несколько советов по оформлению графиков в Excel:

Первое, что следует сделать пользователю, — ввести правильно название зависимости. Для этого нужно выделить щелчком мыши блок «Название диаграммы», щёлкнуть по нему ещё раз и ввести требуемое наименование. При необходимости этот блок можно удалить, выделив его и нажав клавишу Delete.

Если требуется изменить не только название, но и стиль написания, следует, снова выделив блок, вызвать контекстное меню и выбрать в нём раздел «Шрифт». Подобрав подходящий вариант, юзер может нажимать на «ОК» и переходить к дальнейшим действиям.

Вызвав меню «Формат названия диаграммы», можно определить, в какой части рисунка будет располагаться наименование: в центре, в левом верхнем, нижнем правом углу и так далее.

Чтобы добавить на график названия осей, следует щёлкнуть мышью по «плюсику» справа от рисунка и в выплывающем списке установить галочку в соответствующем чекбоксе.

Если изначальное расположение названий не устраивает пользователя, он может свободно перетаскивать их по полю графика, а также менять их наименования описанным ранее способом.

Чтобы добавить на любую линию графика подписи (размещаются прямо на сетке) или выноски данных (в отдельных окошечках), нужно выделить её щелчком правой клавишей мыши и выбрать соответствующий параметр во вложенном меню «Добавить подписи данных».

Юзер может свободно сочетать способы размещения подписей, выбирая любой из пунктов в расширенном меню окошка «Элементы диаграммы».

Выбрав в том же меню «Дополнительные параметры», в боковом меню следует указать категорию представленных данных: простые числа, дроби, проценты, деньги и так далее.

Чтобы добавить таблицу с данными непосредственно на график, нужно вызвать нажатием на «плюсик» всё те же «Дополнительные параметры» и установить галочку в одноимённом чекбоксе.

Сетку, позволяющую найти значения графика в каждой точке, с помощью того же меню можно совсем убрать или добавить на неё основную и вспомогательную разметку.

«Легенда» — не самый полезный, но привычный блок графиков Excel. Убрать или перенести его можно, сняв галочку в окне «Дополнительные параметры» или вызвав вложенное меню. Более простой вариант — выделить блок щелчком мыши и нажать клавишу Delete или перетащить по полю графика.

Понять общее направление движения графика поможет линия тренда; добавить её для каждого ряда значений можно в том же окне.

Перейдя на вкладку «Конструктор», пользователь может кардинально изменить вид графика, выбрав один из стандартных шаблонов в разделе «Стили диаграмм».

А вызвав находящееся там же меню «Изменить цвета» — подобрать палитру для каждой линии в отдельности или для всего графика в целом.

Меню «Стили» вкладки «Формат» позволяет найти оптимальное представление для текстовых элементов графика.

Изменить фон, оставив нетронутым тип диаграммы, можно с помощью раздела «Стили фигур».

На этом настройку графика можно считать оконченной. Пользователь может в любой момент изменить тип диаграммы, перейдя в одноимённое меню и выбрав понравившийся вариант.

Как построить объемную диаграмму в Excel

Чтобы вставить любую объемную диаграмму, необходимо выделить ряды с исходными данными, перейти на вкладку «Вставка» и выбрать тип в группе «Диаграммы».

Таблица с исходными данными:

Построим на ее основе объемную гистограмму. Выбор для этого типа диаграммы достаточно разнообразен:

В объемных гистограммах появляется третья ось (кроме вертикальной и горизонтальной) – ось глубины. Их все пользователь может изменить. В диаграммах подобного типа сопоставляются значения по горизонтальной оси и оси глубины.

Добавим в таблицу еще один ряд данных.

Построим объемную цилиндрическую гистограмму с тремя осями. С ее помощью сравним точки данных по категориям и по рядам.

В программе Excel есть только один тип объемного графика.

Каждый ряд данных в таком графике представляет собой объемную ленту. Здесь тоже появляется третья ось – ось глубины.

Объемная круговая диаграмма в Excel иллюстрирует вклад каждого значения в общий итог в объемном формате.

Огромное преимущество таких диаграмм – возможность отделить, «вытащить» какую-либо область, чтобы заострить на ней внимание. В объемную круговую диаграмму можно включить только один ряд данных

Посмотрим, как отделяется сектор

В объемную круговую диаграмму можно включить только один ряд данных. Посмотрим, как отделяется сектор.

Добавим подписи данных на области круга (выделить диаграмму – перейти на вкладку «Макет» — «Подписи данных»).

Заострим внимание на товаре, который в анализируемом периоде продавался хуже всего. Щелкнем мышкой по сектору с надписью «19»

И, удерживая мышкой данную область, протянем ее в сторону.

Чтобы сектора были хорошо видны, немного развернем их, изменим перспективу объемной фигуры. Снова заходим на вкладку «Макет». Выбираем «Поворот объемной фигуры» в группе «Фон». Передвигаем открывшееся окно так, чтобы была видна диаграмма. Устанавливаем градусы поворота, отображения горизонтальной и вертикальной оси.

В примере так:

Фигура больше развернулась к нам «лицом»:

Для выделения каждого значения в общей сумме данных применяется объемная разрезанная круговая диаграмма.

В данном случае перемещать вручную области невозможно. Но изменять настройки разреза для отдельного либо для каждого сектора можно.

Сгруппированные линейчатые объемные диаграммы в Excel дают возможность пользователю сопоставить величины по категориям. На подобных графиках категории отображаются по вертикали, а значения – по горизонтали.

В таких диаграммах применяются объемные прямоугольники с горизонтальным направлением. Но выполнить трехмерную проекцию с использованием данного типа нельзя (ось глубины отсутствует).

Чтобы показать вклад каждой величины из ряда данных в общую сумму значений, применяют объемную линейчатую диаграмму с накоплением.

Другие горизонтальные виды объемных форматов – цилиндрические, конические, пирамидальные. Доступны те же варианты: с группировкой, с накоплением, нормированные с накоплением (для вывода доли в процентах).

Объемная диаграмма с областями показывает изменение значения с течением времени либо по подгруппам. В нашем примере – по видам товаров.

В диаграмме с областями тоже имеется ось глубины, которая меняется при необходимости.

Самым привлекательным трехмерным изображением является поверхностная диаграмма. Для наших рядов данных она будет выглядеть так:

Поверхностная диаграмма позволяет сопоставить два набора данных и найти оптимальные комбинации. Одна величина имеет два измерения. Ее изменение показано в виде поверхности. Цветные полосы разделяют значения, а не отображают ряда данных.

Такие диаграммы хорошо использовать для визуализации зависимости между большими объемами значений. Когда другие типы просто не подходят.

Построение графиков других функций

Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.

Квадратичная функция  y=ax2+bx+c

Выполните следующие действия:

• В первой строке меняем заголовок
• В третьей строке указываем коэффициенты и их значения
• В ячейку A6 записываем обозначение функции
• В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
• Копируем её на весь диапазон значений аргумента вправо

Получаем результат

График квадратичной функции

Кубическая парабола  y=ax3

Для построения выполните следующие действия:

• В первой строке меняем заголовок
• В третьей строке указываем коэффициенты и их значения
• В ячейку A6 записываем обозначение функции
• В ячейку B6 вписываем формулу =$B3*B5*B5*B5
• Копируем её на весь диапазон значений аргумента вправо

Получаем результат

График кубической параболы

Гипербола  y=k/x

Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.

Далее выполните действия:

• В первой строке меняем заголовок.
• В третьей строке указываем коэффициенты и их значения.
• В ячейку A6 записываем обозначение функции.
• В ячейку B6 вписываем формулу =$B3/B5
• Копируем её на весь диапазон значений аргумента вправо.
• Удаляем формулу из ячейки I6.

Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.

• Кликните диаграмму
• На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
• Откроется окно мастера ввода данных
• Выделите мышкой прямоугольный диапазон ячеек A5:P6
• Нажмите ОК в окне мастера.

Получаем результат

График гиперболы

Построение тригонометрических функций sin(x) и cos(x)

Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x). Сначала заполните таблицу как на рисунке ниже

Таблица значений функции sin(x)

В первой строке записано название тригонометрической функции. В третьей строке прописаны коэффициенты и их значения

Обратите внимание на ячейки, в которые вписаны значения коэффициентов. В пятой строке таблицы прописываются значения углов в радианах

Эти значения будут использоваться для подписей на графике. В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; … В седьмой строке записываются расчетные формулы тригонометрической функции.

Запись расчетной формулы функции sin(x) в Excel

В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице. После заполнения таблицы приступаем к построению графика.

Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами. 

Построение диаграммы Точечная с гладкими кривыми

В итоге получим диаграмму.

График sin(x) после вставки диаграммы

Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.

Настройка сетки при построении графика

Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.

Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.

Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.

Настройка формата горизонтальной оси Х графика функции

Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5. Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.

Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.

Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.

PS: Интересные факты про логотипы известных компаний

Построение графика по точкам

Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)

Рис. 1. Создание матриц-столбцов

В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «». У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.

Рис. 2. Заполнение матриц-столбцов для графика

На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)

Рис. 3. Создание заготовки для графика

Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)

Рис. 4. График по точкам

Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)

Рис. 5. Настройка отображения графика

Создание параболы

Парабола представляет собой график квадратичной функции следующего типа f(x)=ax^2+bx+c. Одним из примечательных его свойств является тот факт, что парабола имеет вид симметричной фигуры, состоящей из набора точек равноудаленных от директрисы. По большому счету построение параболы в среде Эксель мало чем отличается от построения любого другого графика в этой программе.

Создание таблицы

Прежде всего, перед тем, как приступить к построению параболы, следует построить таблицу, на основании которой она и будет создаваться. Для примера возьмем построение графика функции f(x)=2x^2+7.

1. Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».

Выполняется активация окна регулировки прогрессии. В блоке «Расположение» следует переставить кнопку в позицию «По столбцам», так как ряд «X» размещается именно в столбце, хотя в других случаях, возможно, нужно будет выставить переключатель в позицию «По строкам». В блоке «Тип» оставляем переключатель в позиции «Арифметическая».

В поле «Шаг» вводим число «1». В поле «Предельное значение» указываем число «10», так как мы рассматриваем диапазон x от -10 до 10 включительно. Затем щелкаем по кнопке «OK».

После этого действия весь столбец «X» будет заполнен нужными нам данными, а именно числами в диапазоне от -10 до 10 с шагом 1.

Теперь нам предстоит заполнить данными столбец «f(x)». Для этого, исходя из уравнения (f(x)=2x^2+7), нам нужно вписать в первую ячейку данного столбца выражение по следующему макету:

Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:

Теперь нам нужно скопировать формулу и на весь нижний диапазон данного столбца. Учитывая основные свойства Excel, при копировании все значения x будут поставлены в соответствующие ячейки столбца «f(x)» автоматически. Для этого ставим курсор в правый нижний угол ячейки, в которой уже размещена формула, записанная нами чуть ранее. Курсор должен преобразоваться в маркер заполнения, имеющий вид маленького крестика. После того, как преобразование произошло, зажимаем левую кнопку мыши и тянем курсор вниз до конца таблицы, после чего отпускаем кнопку.

Как видим, после этого действия столбец «f(x)» тоже будет заполнен.

На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.

Урок: Как сделать автозаполнение в Экселе

Построение графика

Как уже было сказано выше, теперь нам предстоит построить сам график.

1. Выделяем таблицу курсором, зажав левую кнопку мыши. Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.

Как видим, после этих действий, парабола построена.

Урок: Как сделать диаграмму в Экселе

Редактирование диаграммы

Теперь можно немного отредактировать полученный график.

1. Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».

Открывается окно выбора типов диаграмм. Выбираем наименование «Точечная с гладкими кривыми и маркерами». После того, как выбор сделан, выполняем щелчок по кнопке «OK».

Теперь график параболы имеет более привычный вид.

Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.

Урок: Как подписать оси диаграммы в Excel

Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.