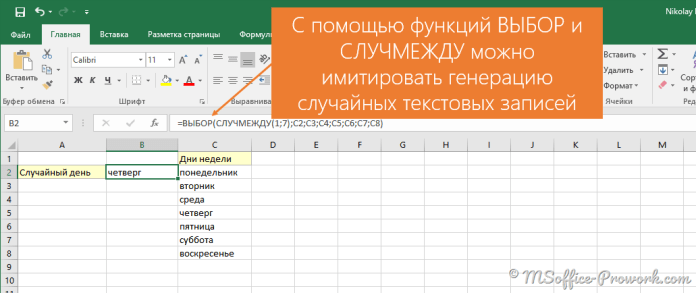
Теория вероятностей на практике или знаете ли вы о random

Examples¶

Basic examples:

>>> random()                             # Random float:  0.0 <= x < 1.0
0.37444887175646646

>>> uniform(2.5, 10.0)                   # Random float:  2.5 <= x < 10.0
3.1800146073117523

>>> expovariate(1  5)                   # Interval between arrivals averaging 5 seconds
5.148957571865031

>>> randrange(10)                        # Integer from 0 to 9 inclusive
7

>>> randrange(, 101, 2)                 # Even integer from 0 to 100 inclusive
26

>>> choice()      # Single random element from a sequence
'draw'

>>> deck = 'ace two three four'.split()
>>> shuffle(deck)                        # Shuffle a list
>>> deck


>>> sample(, k=4)    # Four samples without replacement

Simulations:

>>> # Six roulette wheel spins (weighted sampling with replacement)
>>> choices(, 18, 18, 2], k=6)


>>> # Deal 20 cards without replacement from a deck
>>> # of 52 playing cards, and determine the proportion of cards
>>> # with a ten-value:  ten, jack, queen, or king.
>>> dealt = sample(, counts=16, 36], k=20)
>>> dealt.count('tens')  20
0.15

>>> # Estimate the probability of getting 5 or more heads from 7 spins
>>> # of a biased coin that settles on heads 60% of the time.
>>> def trial():
...     return choices('HT', cum_weights=(0.60, 1.00), k=7).count('H') >= 5
...
>>> sum(trial() for i in range(10_000))  10_000
0.4169

>>> # Probability of the median of 5 samples being in middle two quartiles
>>> def trial():
...     return 2_500 <= sorted(choices(range(10_000), k=5))[2 < 7_500
...
>>> sum(trial() for i in range(10_000))  10_000
0.7958

Example of statistical bootstrapping using resampling
with replacement to estimate a confidence interval for the mean of a sample:

# http://statistics.about.com/od/Applications/a/Example-Of-Bootstrapping.htm
from statistics import fmean as mean
from random import choices

data = 41, 50, 29, 37, 81, 30, 73, 63, 20, 35, 68, 22, 60, 31, 95
means = sorted(mean(choices(data, k=len(data))) for i in range(100))
print(f'The sample mean of {mean(data).1f} has a 90% confidence '
      f'interval from {means5.1f} to {means94.1f}')

Example of a
to determine the statistical significance or p-value of an observed difference
between the effects of a drug versus a placebo:

# Example from "Statistics is Easy" by Dennis Shasha and Manda Wilson
from statistics import fmean as mean
from random import shuffle

drug = 54, 73, 53, 70, 73, 68, 52, 65, 65
placebo = 54, 51, 58, 44, 55, 52, 42, 47, 58, 46
observed_diff = mean(drug) - mean(placebo)

n = 10_000
count = 
combined = drug + placebo
for i in range(n):
    shuffle(combined)
    new_diff = mean(combined) - mean(combinedlen(drug):])
    count += (new_diff >= observed_diff)

print(f'{n} label reshufflings produced only {count} instances with a difference')
print(f'at least as extreme as the observed difference of {observed_diff.1f}.')
print(f'The one-sided p-value of {count  n.4f} leads us to reject the null')
print(f'hypothesis that there is no difference between the drug and the placebo.')

Simulation of arrival times and service deliveries for a multiserver queue:

from heapq import heappush, heappop
from random import expovariate, gauss
from statistics import mean, median, stdev

average_arrival_interval = 5.6
average_service_time = 15.0
stdev_service_time = 3.5
num_servers = 3

waits = []
arrival_time = 0.0
servers = 0.0 * num_servers  # time when each server becomes available
for i in range(100_000):
    arrival_time += expovariate(1.0  average_arrival_interval)
    next_server_available = heappop(servers)
    wait = max(0.0, next_server_available - arrival_time)
    waits.append(wait)
    service_duration = gauss(average_service_time, stdev_service_time)
    service_completed = arrival_time + wait + service_duration
    heappush(servers, service_completed)

print(f'Mean wait: {mean(waits).1f}.  Stdev wait: {stdev(waits).1f}.')
print(f'Median wait: {median(waits).1f}.  Max wait: {max(waits).1f}.')

How Math.random() is implemented

The Math.random() method internally creating a single new pseudorandom-number generator, exactly as if by the expression new java.util.Random(). This new pseudorandom-number generator is used thereafter for all calls to this method and is used nowhere else. The nextDouble() method of Random class is called on this pseudorandom-number generator object.

This method is properly synchronized to allow correct use by more than one thread. However, if many threads need to generate pseudorandom numbers at a great rate, it may reduce contention for each thread to have its own pseudorandom-number generator.

As the largest double value less than 1.0 is Math.nextDown(1.0), a value x in the closed range where x1<=x2 may be defined by the statements.

❮ Math.round()
Java Tutorial ❯

Модуль random

Для того, чтобы полноценно использовать эту опцию в своей работе, необходимо ознакомится с главными ее составляющими. Они выступают некими методами, позволяющими выполнять определенные действия. Основная стандартная библиотека Рython состоит из таких компонентов со следующими параметрами:

• random () – может вернуть число в промежуток значений от 0 до 1;
• seed (a) – производит настройку генератора на новую последовательность а;
• randint (a,b) – возвращает значение в диапазон данных от а до b;
• randrange (a, b, c) – выполняет те же функции, что и предыдущая, только с шагом с;
• uniform (a, b) – производит возврат вещественного числа в диапазон от а до b;
• shuffle (a) – миксует значения, находящиеся в перечне а;
• choice (a) – восстанавливает обратно случайный элемент из перечня а;
• sample (a, b) – возвращает на исходную позицию последовательность длиной b из перечня а;
• getstate () – обновляет внутреннее состояние генератора;
• setstate (a) – производит восстановление внутреннего состояния генератора а;
• getrandbits (a) – восстанавливает а при выполнении случайного генерирования бит;
• triangular (a, b, c) – показывает изначальное значение числа от а до b с шагом с.

Если вам необходимо применить для задания инициализирующееся число псевдо случайной последовательности, то не обойтись без функции seed. После ее вызова без применения параметра, используется значение системного таймера. Эта опция доступна в конструкторе класса Random.

Более показательными будут примеры на основе вышеописанного материала. Для возможности воспользоваться генерацией случайных чисел в Рython 3, сперва вам потребуется выполнить импорт библиотеки random, внеся сперва ее в начало исполняемого файла при помощи ключевого слова import.

Вещественные числа

Модуль оснащен одноименной функцией random. Она более активно используется в Питоне, чем остальные. Эта функция позволяет произвести возврат числа в промежуток значений от 0 до 1. Вот пример трех основных переменных:

import randoma = random.random()b = random.random()print(a)print(b)

0.5479332865190.456436031781

Целые числа

Чтобы в программе появились случайные числа из четко заданного диапазона, применяется функция randit. Она обладает двумя аргументами: максимальным и минимальным значением. Она отображает значения, указанные ниже в генерации трех разных чисел от 0 до 9.

import randoma = random.randint(0, 9)b = random.randint(0, 9)print(a)print(b)

47

Диапазон целых чисел

Использование в такой ситуации метода randage поможет сгенерировать целочисленные значения, благодаря сотрудничеству с тремя основными параметрами:

• минимальное значение;
• максимальное;
• длина шага.

При вызове функции с одним требованием, граница будет установлена на значении 0, а промежуток будет установлен на 1. Для двух аргументов длина шага уже высчитывается автоматически. Вот пример работы этой опции на основе трех разных наборов.

import randoma = random.randrange(10)b = random.randrange(2, 10)c = random.randrange(2, 10, 2)print(a)print(b)print(c)

952

Диапазон вещественных чисел

Генерация вещественных чисел происходит при использовании функции под названием uniform. Она регулируется всего двумя параметрами: минимальным и максимальным значением. Пример создания демонстрации с переменными a, b и c.

import randoma = random.uniform(0, 10)b = random.uniform(0, 10)print(a)print(b)

4.856873750913.66695202551

Генерация случайного n-мерного массива вещественных чисел

• Использование для генерации n-мерного массива случайных вещественных чисел в пределах
• Использование для генерации n-мерного массива случайных вещественных чисел в пределах

Python

import numpy

random_float_array = numpy.random.rand(2, 2)
print(«2 X 2 массив случайных вещественных чисел в \n», random_float_array,»\n»)

random_float_array = numpy.random.uniform(25.5, 99.5, size=(3, 2))
print(«3 X 2 массив случайных вещественных чисел в \n», random_float_array,»\n»)

1 2 3 4 5 6 7 8

importnumpy random_float_array=numpy.random.rand(2,2) print(«2 X 2 массив случайных вещественных чисел в \n»,random_float_array,»\n») random_float_array=numpy.random.uniform(25.5,99.5,size=(3,2)) print(«3 X 2 массив случайных вещественных чисел в \n»,random_float_array,»\n»)

Вывод:

Shell

2 X 2 массив случайных вещественных чисел в

]

3 X 2 массив случайных вещественных чисел в

]

1 2 3 4 5 6 7 8

2X2массивслучайныхвещественныхчиселв0.0,1.0 0.089385930.89085866 0.473071690.41401363 3X2массивслучайныхвещественныхчиселв25.5,99.5 55.405785465.60206715 91.6218540484.16144062 44.34825227.28381058

Придумываем свой алгоритм ГПСЧ

Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.

А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:

Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9.

Мы получили генератор чисел от 0 до 9, но распределение очень неравномерное и каждый раз он будет генерировать одну и ту же последовательность.

Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:

Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random() — это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.

Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них — это Линейный конгруэнтный ГПСЧ(LCPRNG).

Bias

In Node.js, the most widely available CSPRNG is the function, but you shouldn’t use this directly, as it’s easy to mess up and «bias» your random values — that is, making it more likely that a specific value or set of values is picked.

A common example of this mistake is using the modulo operator when you have less than 256 possibilities (since a single byte has 256 possible values). Doing so actually makes lower values more likely to be picked than higher values.

For example, let’s say that you have 36 possible random values — plus every lowercase letter in . A naive implementation might look something like this:

let randomCharacter = randomByte % 36;

That code is broken and insecure. With the code above, you essentially create the following ranges (all inclusive):

• 0-35 stays 0-35.
• 36-71 becomes 0-35.
• 72-107 becomes 0-35.
• 108-143 becomes 0-35.
• 144-179 becomes 0-35.
• 180-215 becomes 0-35.
• 216-251 becomes 0-35.
• 252-255 becomes 0-3.

If you look at the above list of ranges you’ll notice that while there are 7 possible values for each between 4 and 35 (inclusive), there are 8 possible values for each between 0 and 3 (inclusive). This means that while there’s a 2.64% chance of getting a value between 4 and 35 (inclusive), there’s a 3.02% chance of getting a value between 0 and 3 (inclusive).

This kind of difference may look small, but it’s an easy and effective way for an attacker to reduce the amount of guesses they need when bruteforcing something. And this is only one way in which you can make your random values insecure, despite them originally coming from a secure random source.

The Rolling Dice Game

In this section, we will create a really simple mini dice game. Two players enter their name and will roll the dice. The player whose dice has a higher number will win the round.

First, create a function that simulates the action for rolling the dice.

Inside the function body, call the function with and as the arguments. This will give you any random number between 1 and 6 (both inclusive) just like how real dice would work.

Next, create two input fields and a button as shown below:

When the ‘Roll Dice’ button is clicked, get the player names from the input fields and call the function for each player.

You can validate the players’ name fields and prettify the markup with some CSS. For the purpose of brevity, I’m keeping it simple for this guide.

That is it. You can check out the demo here.

Псевдослучайные числа

Иногда программист сталкивается с простыми, казалось бы, задачами: «отобрать случайный фильм для вечернего просмотра из определенного списка», «выбрать победителя лотереи», «перемешать список песен при тряске смартфона», «выбрать случайное число для шифрования сообщения», и каждый раз у него возникает очень закономерный вопрос: а как получить это самое случайное число?

Вообще-то, если вам нужно получить «настоящее случайное число», сделать это довольно-таки трудно. Вплоть до того, что в компьютер встраивают специальные математические сопроцессоры, которые умеют генерировать такие числа, с выполнением всех требований к «истинной случайности».

Поэтому программисты придумали свое решение — псевдослучайные числа. Псевдослучайные числа — это некая последовательность, числа в которой на первый взгляд кажутся случайными, но специалист при детальном анализе сможет найти в них определенные закономерности. Для шифрования секретных документов такие числа не подойдут, а для имитации бросания кубика в игре — вполне.

Есть много алгоритмов генерации последовательности псевдослучайных чисел и почти все из них генерируют следующее случайное число на основе предыдущего и еще каких-то вспомогательных чисел.

Например, данная программа выведет на экран неповторяющихся чисел:

Кстати, мы говорим не о псевдослучайных числах, а именно о последовательности таких чисел. Т.к. глядя на одно число невозможно понять, случайное оно или нет.

Случайное число ведь можно получить разными способами:

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:

Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).

Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ — это проблема. Если говорить про другие задачи, то эти свойства — могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.

Еще одно свойство — воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.

Usage

node.js

In your project, run the following command:

npm install random-js

or

yarn add random-js

In your code:

// ES6 Modules
import { Random } from "random-js";
const random = new Random(); // uses the nativeMath engine
const value = random.integer(1, 100);

// CommonJS Modules
const { Random } = require("random-js");
const random = new Random(); // uses the nativeMath engine
const value = random.integer(1, 100);

Or to have more control:

const Random = require("random-js").Random;
const random = new Random(MersenneTwister19937.autoSeed());
const value = random.integer(1, 100);

It is recommended to create one shared engine and/or instance per-process rather than one per file.

Browser using AMD or RequireJS

Download and place it in your project, then use one of the following patterns:

define(function(require) {
  var Random = require("random");
  return new Random.Random(Random.MersenneTwister19937.autoSeed());
});

define(function(require) {
  var Random = require("random");
  return new Random.Random();
});

define("random", function(Random) {
  return new Random.Random(Random.MersenneTwister19937.autoSeed());
});

Browser using tag

Download and place it in your project, then add it as a tag as such:

<script src="lib/random-js.min.js"></script>
<script>
  // Random is now available as a global (on the window object)
  var random = new Random.Random();
  alert("Random value from 1 to 100: " + random.integer(1, 100));
</script>

Why is this needed?

Despite being capable of producing numbers within [0, 1), there are a few downsides to doing so:

• It is inconsistent between engines as to how many bits of randomness:
  • Internet Explorer: 53 bits
  • Mozilla Firefox: 53 bits
  • Google Chrome/node.js: 32 bits
  • Apple Safari: 32 bits
• It is non-deterministic, which means you can’t replay results consistently
• In older browsers, there can be manipulation through cross-frame random polling. This is mostly fixed in newer browsers and is required to be fixed in ECMAScript 6.

Also, and most crucially, most developers tend to use improper and biased logic as to generating integers within a uniform distribution.

Using Third-Party APIs

As we have seen, Java provides us with a lot of classes and methods for generating random numbers. However, there are also third-party APIs for this purpose.

We’re going to take a look at some of them.

3.1. org.apache.commons.math3.random.RandomDataGenerator

There are a lot of generators in the commons mathematics library from the Apache Commons project. The easiest, and probably the most useful, is the RandomDataGenerator. It uses the Well19937c algorithm for the random generation. However, we can provide our algorithm implementation.

Let’s see how to use it. Firstly, we have to add dependency:

The latest version of commons-math3 can be found on Maven Central.

Then we can start working with it:

3.2. it.unimi.dsi.util.XoRoShiRo128PlusRandom

Certainly, this is one of the fastest random number generator implementations. It has been developed at the Information Sciences Department of the Milan University.

The library is also available at Maven Central repositories. So, let’s add the dependency:

This generator inherits from java.util.Random. However, if we take a look at the JavaDoc, we realize that there’s only one way of using it —  through the nextInt method. Above all, this method is only available with the zero- and one-parameter invocations. Any of the other invocations will directly use the java.util.Random methods.

For example, if we want to get a random number within a range, we would write:

Генерация случайных чисел в заданном диапазоне

Существует несколько способов генерации случайного (псевдослучайного) числа:

1. Использование метода random() из класса математических функций Math , находящемся в пакете java.lang.

1. Использование метода random() из класса Random , находящемся в пакете java.util.Random.

1. Использование генератора случайных чисел класса SecureRandom , предназначенного для целей криптографии и, находящегося в пакете java.security. SecureRandom (здесь не рассматривается).

Рассмотрим методы генерации случайных чисел.

Класс Math. Метод random()

Метод random() класса Math возвращает псевдослучайное число типа double в диапазоне 0 ≤ Math.random()

Пример 1. Несколько случайных чисел

Случайное число № 1: 0.9161994380531232 Случайное число № 2: 0.24340742865928744 Случайное число № 3: 0.9783627451986034

Пример 2. Случайное число x в диапазоне a ≤ x ≤ b

Для генерации целого случайного числа x в заданном диапазоне a ≤ x ≤ b, обычно используется следующая зависимость:

x = a + (int)(Math.random()*((b — a) + 1)).

Получим случайное число x в диапазоне: 10 ≤ x ≤ 20 (a=10, b=20).

Результат.Случайное число x: 19

Класс Random. Метод random()

Это наиболее часто используемый класс для генерации псевдослучайный чисел с равномерной функцией распределения. Имеется метод nextGaussian() , который моделирует функцию нормального распределения.

Основными методами этого класса являются:

• int nextInt( ) — возвращает следующее случайное значение ix типа int в диапазоне -2147483648 ≤ ix
• int nextInt(int n) — возвращает следующее случайное значение ix типа int в диапазоне 0 ≤ ix
• float nextFloat() — возвращает следующее случайное значение fx типа float в диапазоне 0.0 ≤ fx
• double nextDouble() — возвращает следующее случайное значение dx типа double в диапазоне 0.0 ≤ dx
• boolean nextBoolean() — возвращает следующее случайное значение типа boolean

Для получения случайных чисел необходимо:

1. Подключить библиотеку случайных чисел. Пишем до определения класса. import java.util.Random;
2. В классе создать объект rand случайных чисел Random rand = new Random();
3. Далее использовать необходимые методы объекта rand.

Пример 1. Несколько случайных чисел разных типов.

Случайное число ix: 1438841988 Случайное число dx: 0.6120986135409442 Случайное число fx: 0.103119016 Случайное число bx: true

Пример 2. Случайное число x в диапазоне a ≤ x ≤ b.

Для генерации целого случайного числа x в заданном диапазоне a ≤ x ≤ b, обычно используется следующая зависимость:

тип int int x = a + rand.nextInt(b — a + 1).

тип double double y = a + rand.nextInt(b — a).

Случайное число x: 12 Случайное число dx: 17.505847041626733

Для типа double будет выведено случайное число в виде:

что неудобно. Для приемлемого представления используется форматный вывод, позволяющий выводить числа с заданной точностью.

Форматный вывод

Пакет java.io содержит класс PrintStream , который содержит методы printf и forma t, позволяющие выводить числа с заданной точностью. Рассмотрим метод format(). Синтаксис метода

System.out.format(String format, Object. args),

format — это строка — шаблон, согласно которому будет происходить форматирование, args — это список переменных, для вывода по заданному шаблону.

Строка — шаблон содержит обычный текст и специальные форматирующие символы. Эти символы начинаются со знака процента (%) и заканчиваются конвертором — символом, который определяет тип переменной для форматирования. Вот некоторые конверторы:

Источник

Using Java API

The Java API provides us with several ways to achieve our purpose. Let’s see some of them.

2.1. java.lang.Math

The random method of the Math class will return a double value in a range from 0.0 (inclusive) to 1.0 (exclusive). Let’s see how we’d use it to get a random number in a given range defined by min and max:

2.2. java.util.Random

Before Java 1.7, the most popular way of generating random numbers was using nextInt. There were two ways of using this method, with and without parameters. The no-parameter invocation returns any of the int values with approximately equal probability. So, it’s very likely that we’ll get negative numbers:

If we use the netxInt invocation with the bound parameter, we’ll get numbers within a range:

This will give us a number between 0 (inclusive) and parameter (exclusive). So, the bound parameter must be greater than 0. Otherwise, we’ll get a java.lang.IllegalArgumentException.

Java 8 introduced the new ints methods that return a java.util.stream.IntStream. Let’s see how to use them.

The ints method without parameters returns an unlimited stream of int values:

We can also pass in a single parameter to limit the stream size:

And, of course, we can set the maximum and minimum for the generated range:

2.3. java.util.concurrent.ThreadLocalRandom

Java 1.7 release brought us a new and more efficient way of generating random numbers via the ThreadLocalRandom class. This one has three important differences from the Random class:

• We don’t need to explicitly initiate a new instance of ThreadLocalRandom. This helps us to avoid mistakes of creating lots of useless instances and wasting garbage collector time
• We can’t set the seed for ThreadLocalRandom, which can lead to a real problem. If we need to set the seed, then we should avoid this way of generating random numbers
• Random class doesn’t perform well in multi-threaded environments

Now, let’s see how it works:

With Java 8 or above, we have new possibilities. Firstly, we have two variations for the nextInt method:

Secondly, and more importantly, we can use the ints method:

2.4. java.util.SplittableRandom

Java 8 has also brought us a really fast generator — the SplittableRandom class.

As we can see in the JavaDoc, this is a generator for use in parallel computations. It’s important to know that the instances are not thread-safe. So, we have to take care when using this class.

We have available the nextInt and ints methods. With nextInt we can set directly the top and bottom range using the two parameters invocation:

This way of using checks that the max parameter is bigger than min. Otherwise, we’ll get an IllegalArgumentException. However, it doesn’t check if we work with positive or negative numbers. So, any of the parameters can be negative. Also, we have available one- and zero-parameter invocations. Those work in the same way as we have described before.

We have available the ints methods, too. This means that we can easily get a stream of int values. To clarify, we can choose to have a limited or unlimited stream. For a limited stream, we can set the top and bottom for the number generation range:

2.5. java.security.SecureRandom

If we have security-sensitive applications, we should consider using SecureRandom. This is a cryptographically strong generator. Default-constructed instances don’t use cryptographically random seeds. So, we should either:

• Set the seed — consequently, the seed will be unpredictable
• Set the java.util.secureRandomSeed system property to true

This class inherits from java.util.Random. So, we have available all the methods we saw above. For example, if we need to get any of the int values, then we’ll call nextInt without parameters:

On the other hand, if we need to set the range, we can call it with the bound parameter:

We must remember that this way of using it throws IllegalArgumentException if the parameter is not bigger than zero.

Types of «random»

There exist roughly three types of «random»:

• Truly random: Exactly as the name describes. True randomness, to which no pattern or algorithm applies. It’s debatable whether this really exists.
• Unpredictable: Not truly random, but impossible for an attacker to predict. This is what you need for security-related code — it doesn’t matter how the data is generated, as long as it can’t be guessed.
• Irregular: This is what most people think of when they think of «random». An example is a game with a background of a star field, where each star is drawn in a «random» position on the screen. This isn’t truly random, and it isn’t even unpredictable — it just doesn’t look like there’s a pattern to it, visually.

Irregular data is fast to generate, but utterly worthless for security purposes — even if it doesn’t seem like there’s a pattern, there is almost always a way for an attacker to predict what the values are going to be. The only realistic usecase for irregular data is things that are represented visually, such as game elements or randomly generated phrases on a joke site.

Unpredictable data is a bit slower to generate, but still fast enough for most cases, and it’s sufficiently hard to guess that it will be attacker-resistant. Unpredictable data is provided by what’s called a CSPRNG.

Usage

In your project, run the following command:

npm install random-js

or

yarn add random-js

In your code:

import{Random}from"random-js";constrandom=newRandom();constvalue=random.integer(1,100);

const{Random}=require("random-js");constrandom=newRandom();constvalue=random.integer(1,100);

Or to have more control:

constRandom=require("random-js").Random;constrandom=newRandom(MersenneTwister19937.autoSeed());constvalue=random.integer(1,100);

It is recommended to create one shared engine and/or instance per-process rather than one per file.

Download and place it in your project, then use one of the following patterns:

define(function(require){var Random =require("random");returnnewRandom.Random(Random.MersenneTwister19937.autoSeed());});define(function(require){var Random =require("random");returnnewRandom.Random();});define("random",function(Random){returnnewRandom.Random(Random.MersenneTwister19937.autoSeed());});

Download and place it in your project, then add it as a tag as such:

<scriptsrc="lib/random-js.min.js"><script><script>var random =newRandom.Random();alert("Random value from 1 to 100: "+random.integer(1,100));</script>

Node.js Series Overview

Prev
|
Next

1. Increase the Memory Limit for Your Process

2. Why You Should Add “node” in Your Travis Config

3. Create a PDF from HTML with Puppeteer and Handlebars

4. Create Your Own Custom Error

5. Retrieve a Request’s IP Address in Node.js

6. Detect the Node.js Version in a Running Process or App

Prev
|
Next

1. String Replace All Appearances

2. Remove All Whitespace From a String in JavaScript

3. Generate a Random String in Node.js or JavaScript

4. Remove Extra Spaces From a String in JavaScript or Node.js

5. Remove Numbers From a String in JavaScript or Node.js

6. Get the Part Before a Character in a String in JavaScript or Node.js

7. Get the Part After a Character in a String in JavaScript or Node.js

8. How to Check if a Value is a String in JavaScript or Node.js

9. Check If a String Includes All Strings in JavaScript/Node.js/TypeScript

10. Check if a Value is a String in JavaScript and Node.js

11. Limit and Truncate a String to a Given Length in JavaScript and Node.js

Prev
|
Next

1. Filter Data in Streams

Prev
|
Next

1. Get Number of Seconds Since Epoch in JavaScript

2. Get Tomorrow’s Date in JavaScript

3. Increase a Date in JavaScript by One Week

4. Add Seconds to a Date in Node.js and JavaScript

5. Add Month(s) to a Date in JavaScript or Node.js

1. 
   (Coming soon)
   

2. 
   (Coming soon)
   

Prev
|
Next

1. How to Run an Asynchronous Function in Array.map()

2. How to Reset and Empty an Array

3. for…of vs. for…in Loops

4. Clone/Copy an Array in JavaScript and Node.js

5. Get an Array With Unique Values (Delete Duplicates)

6. Sort an Array of Integers in JavaScript and Node.js

7. Sort a Boolean Array in JavaScript, TypeScript, or Node.js

8. Check If an Array Contains a Given Value in JavaScript or Node.js

9. Add an Item to the Beginning of an Array in JavaScript or Node.js

10. Append an Item at the End of an Array in JavaScript or Node.js

11. How to Exit and Stop a for Loop in JavaScript and Node.js

12. Split an Array Into Smaller Array Chunks in JavaScript and Node.js

13. How to Get an Index in a for…of Loop in JavaScript and Node.js
    
    (Coming soon)
    
14. How to Exit, Stop, or Break an Array#forEach Loop in JavaScript or Node.js
    
    (Coming soon)
    

Prev
|
Next

1. Callback and Promise Support in your Node.js Modules

2. Run Async Functions/Promises in Sequence

3. Run Async Functions/Promises in Parallel

4. Run Async Functions in Batches

5. How to Fix “Promise resolver undefined is not a function” in Node.js or JavaScript

6. Detect if Value Is a Promise in Node.js and JavaScript

Prev
|
Next

1. Human-Readable JSON.stringify() With Spaces and Line Breaks

2. Write a JSON Object to a File

3. Create a Custom “toJSON” Function in Node.js and JavaScript

Prev
|
Next

1. Extend Multiple Classes (Multi Inheritance)

2. Retrieve the Class Name at Runtime in JavaScript and Node.js

Prev
|
Next

1. Generate a Random Number in Range With JavaScript/Node.js

Prev
|
Next

1. How to Merge Objects

2. How to Check if an Object is Empty in JavaScript or Node.js

3. How to CamelCase Keys of an Object in JavaScript or Node.js

1. 
   (Coming soon)
   

2. 
   (Coming soon)
   

3. 
   (Coming soon)
   

Prev
|
Next

1. Get a File’s Created Date

2. Get a File’s Last Modified/Updated Date

3. How to Create an Empty File

4. Check If a Path or File Exists

5. How to Rename a File

6. Check If a Path Is a Directory

7. Check If a Path Is a File
   
   (Coming soon)
   
8. Retrieve the Path to the User’s Home Directory
   
   (Coming soon)
   
9. How to Touch a File
   
   (Coming soon)