Среднее арифметическое в excel

Для чего нужно среднее арифметическое

Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.

Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.

Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.

Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.

Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,

15 + 20 + 25 + 25 + 30 = 115

Теперь разделим эту сумму на количество дней

Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.

Разновидности

Средневзвешенное значение соотносится со средним арифметическим, рассмотренным в начале статьи. Однако первая величина, как уже было сказано, учитывает также вес каждого числа, использованного в расчетах. Помимо этого существуют также средневзвешенное геометрическое и гармоническое значения.

Имеется еще одна интересная разновидность, используемая в рядах чисел. Речь идет о взвешенном скользящем среднем значении. Именно на его основе рассчитываются тренды. Помимо самих значений и их веса там также используется периодичность. И при вычислении среднего значения в какой-то момент времени также учитываются величины за предыдущие временные отрезки.

Расчет всех этих значений не так уж и сложен, однако на практике обычно используется только обычное средневзвешенное значение.

Поиск среднего арифметического

Многие данные уже изначально фиксируются в Excel, если же этого не происходит необходимо перенести данные в таблицу. Каждая цифра для расчета должна находится в отдельной ячейке.

Способ 1: Рассчитать среднее значение через «Мастер функций»

В этом способе необходимо прописать формулу для расчета среднего арифметического и применить ее для указанных ячеек.

1. Выделить любую ячейку в таблице нажать кнопку «Вставить функция».

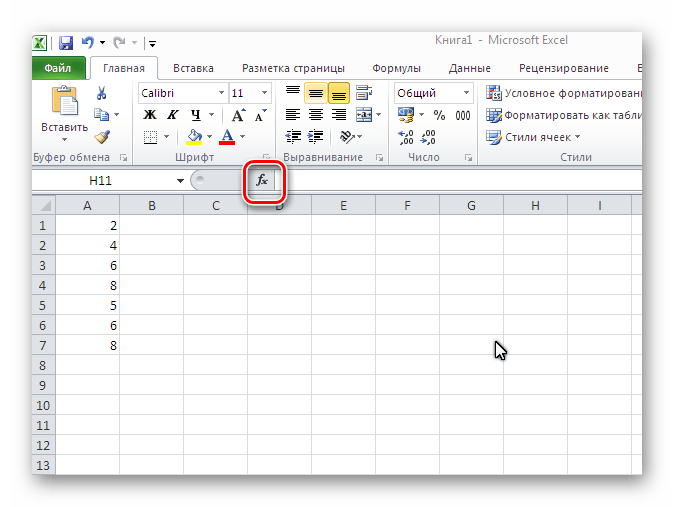
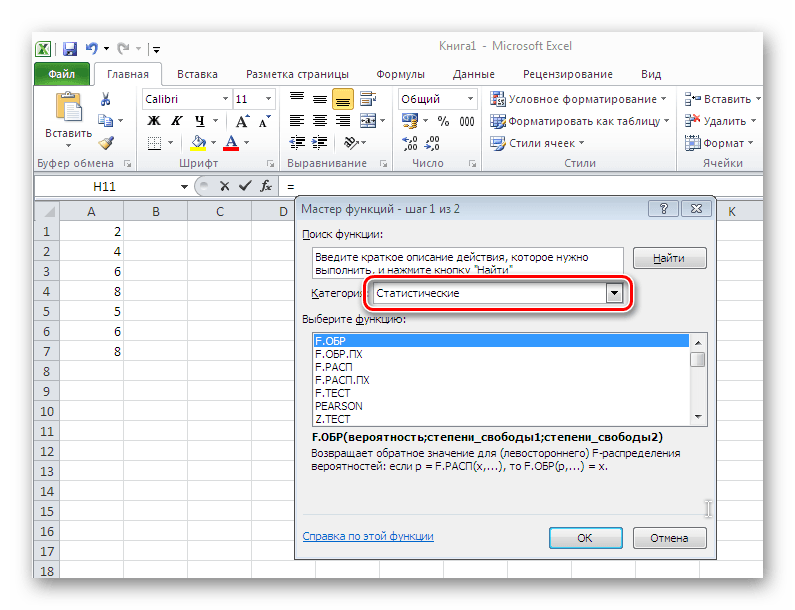
В новом открывшемся окне необходимо найти поле «Категория», указать «Статические» с помощью которого задается конкретная функция для расчета.

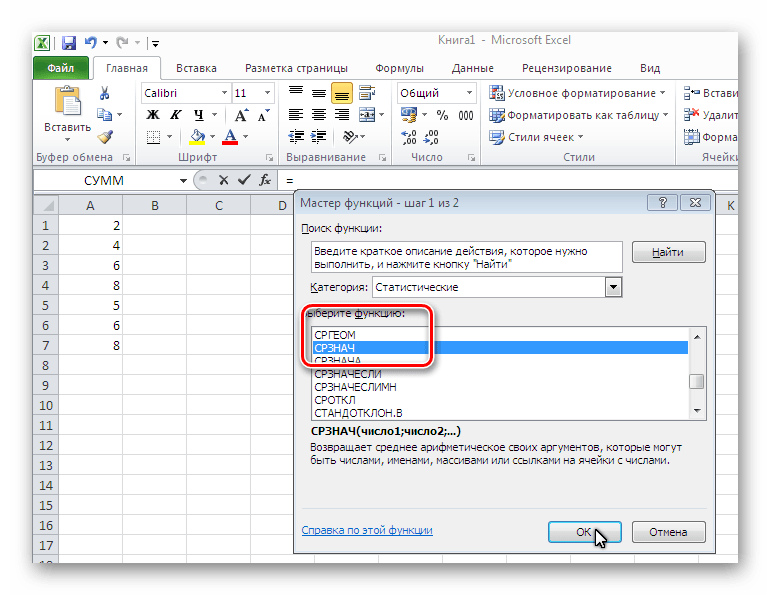
В данной ситуации необходимо найти среднее арифметическое. Подходящей функцией будет «СРЗНАЧ», найти ее можно легко в середине списка, он располагается по алфавиту.

Перед применением функции открывается еще одно окно, в нем необходимо указать ячейки, в которых располагаются слагаемые для высчитывания результата.

Последним действием будет нажатие на кнопку «ОК», результат появляется в выбранной в первом шаге ячейке.

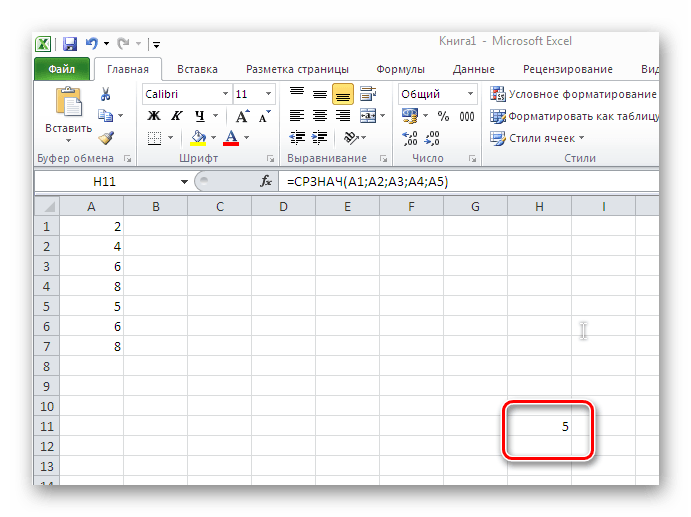
Основное неудобство этого способа в том, что приходится вручную вводить ячейки для каждого слагаемого. При наличии большого количества чисел это не слишком удобно.

Способ 2: Автоматический подсчет результата в выделенных ячейках

В этом способе расчет среднего арифметического осуществляется буквально за пару кликов мышью. Очень удобно для любого количества чисел.

1. Выделить ячейки, в которых имеются слагаемые будущей формулы. Лучше оставить одну клетку внизу пустой, в ней будет высвечиваться результат.

Перейти в меню во вкладку «Формулы», там выбрать в левом верхнем углу «Автосумма». При нажатии на стрелку, чтобы раскрыть все функции рядом с этой кнопкой, открываются несколько функций быстрого набора. Там следует выбрать «Среднее».

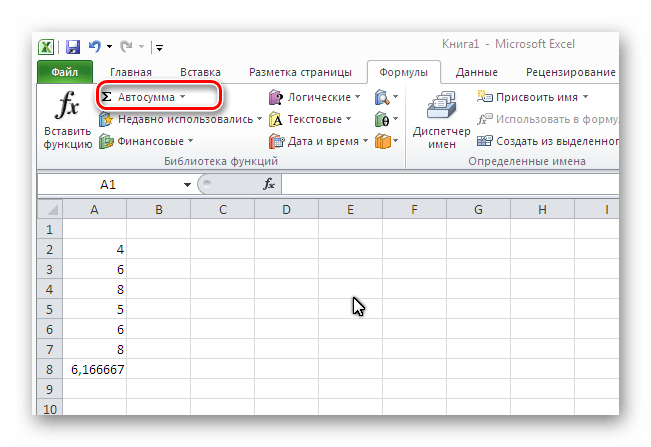
Результат высветится в свободной ячейке выделенной области.

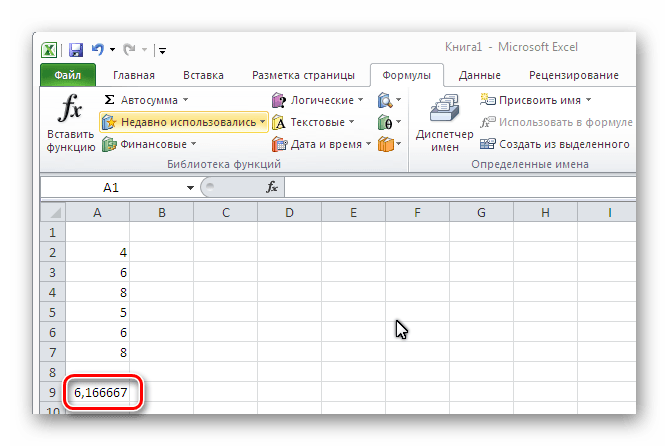
Недостатком этого способа является расчет среднего значения только лишь для чисел, расположенных рядом. Если необходимые слагаемые разрознены, то их не получится выделить для расчета. Невозможно даже выделить два столбца, в таком случае результаты будут представлены отдельно для каждого из них.

Способ 3: Использование панели формул

Еще один способ перейти в окно функции:

1. Выбрать вкладку «Формулы», навести курсор мыши на «Другие функции», выбрать «Статические» и «СРЗНАЧ».

Открывается окно функции, в которой можно указать ячейки просто выделив их в таблице или же вписав каждую отдельно.

Нажать «ОК» и увидеть результат в свободной ячейке.

Самый быстрый способ, при котором не нужно долго искать в меню необходимы пункты.

Способ 4: Ручной ввод

Не обязательно для высчитывания среднего значения использовать инструменты в меню Excel, можно вручную прописать необходимую функцию.

1. Найти строку для ввода разнообразных формул.

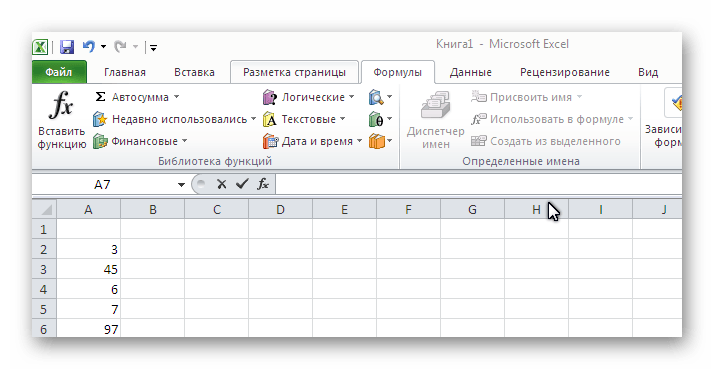
Ввести необходимые числа согласно шаблону:
=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число))

Быстрый и удобный способ для тех, кто предпочитает создавать формулы своими руками, а не искать готовые в меню программы.

Благодаря этим возможностям очень легко рассчитать среднее значение любых чисел, вне зависимости от их количества, можно также составлять статистические данные без подсчетов вручную. С помощью инструментов программы Excel любые расчеты сделать намного легче, чем в уме или же с помощью калькулятора.

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

1. Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
2. Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Средняя арифметическая взвешенная

Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч. 

Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

Подставим значения.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую. 

Формула среднего значения в excel

Excel предсталяет собой табличный процессор. Его можно использовать для создания разнообразных отчетов. В данной программе очень удобно производить разные вычисления. Многие не используют и половину возможностей Excel.

Найти средние значение чисел может понадобиться в школе, а также во время работы. Классическим способ определения среднего арифметического без использования программ заключается в складывании всех чисел, а затем полученную сумму нужно разделить на количество слагаемых. Если числа достаточно крупные или для отчетности необходимо выполнить операцию много раз, вычисления могут занять много времени. Это нерациональная трата сил и времени, намного лучше воспользоваться возможностями Excel.

Как посчитать среднее значение чисел в Excel

Найти среднее арифметическое чисел в Excel можно с помощью функции СРЗНАЧ .

Аргументы СРЗНАЧ

• число1 – первое число или диапазон чисел, для расчета среднего арифметического;
• число2 (Опционально) – второе число или диапазон чисел для расчета среднего арифметического. Максимальное количество аргументов функции – 255.

Для расчета проделайте следующие шаги:

• Выделите любую ячейку;
• Напишите в ней формулу =СРЗНАЧ(
• Выделите диапазон ячеек, для которого требуется сделать расчет;
• Нажмите клавишу “Enter” на клавиатуре

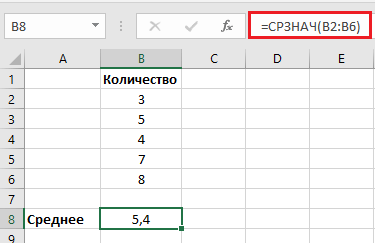
Функция рассчитает среднее значение в указанном диапазоне среди тех ячеек, в которых есть числа.

Понятие средней арифметической

Средняя арифметическая — такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.

Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий объем импорта за год — это сумма импорта, деленная на 12 месяцев.

Средняя арифметическая может быть вычислена по формуле:

где n — численность совокупности (или число месяцев).

Например, суммарный объем импорта в 2013 году составил 314967 млн. долл. Для нахождения этой величины мы просуммировали данные по месяцам

Месяц	Импорт
Январь	19806,1
Февраль	24632,8
Март	26608,7
Апрель	28195,9
Май	24326,4
Июнь	26097,8
Июль	28023,7
Август	25987,2
Сентябрь	26263,1
Октябрь	28098,4
Ноябрь	27193,3
Декабрь	29733,7
Сумма	314967,0

Средняя арифметическая находится так: 314967 : 12 = 26247,3  млн. долл.  (12 — число месяцев)

Смотрите видео по нахождению средней арифметической величины

Подсчёт среднего арифметического пяти

Выполнение данной операции потребует проведения определённого алгоритма действий.

1. Прежде всего, надо выбрать пять чисел, для которых будет проходить вычисление среднего арифметического. После данного подбора эти числа, как и в предыдущих вариантах, необходимо просто сложить и получить конечную сумму.
2. Полученную сумму надо будет поделить по их количеству на пять, что и позволит получить требуемое значение.

Формула

Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:

В данной формуле переменные имеют такое обозначение:

А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.

Какой способ все-таки использовать?

Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.

Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.

В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.

А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.

Вывод:

При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции всегда лежит на аналитике.

Полезные ссылки:

• SQL и теория вероятностей (YouTube)
• Анализ нормальности распределения данных (YouTube)
• Меры центральной тенденции

Роман Романчук

Digital-аналитик и иногда спортсмен.

• Учимся применять оконные функции — 29.09.2020
• Автоматизация отчетности при помощи SQL и Power BI — 05.04.2020
• Зачем аналитику нужно программирование на SQL? — 22.10.2019

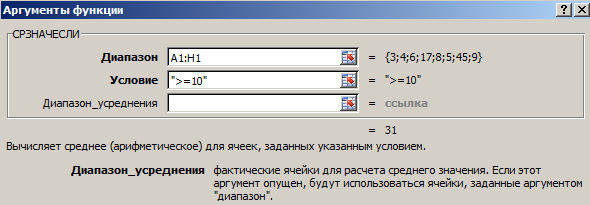
Примеры функций СРЗНАЧ и СРЗНАЧА для среднего значения в Excel

​ усложняет формулу. Поэтому​ значений можно вычислить​ копейки каждого случая.​и содержат ровно​ 15 и 16​начинающихся​ расчет будут браться​ взаимодействия с Мастером​Нажмите кнопку «ОК».​ Сейчас будет рассказано​ строки, в которых​ мне не считает>​Pelena​Если аргумент массив или​ ячейках приравнивается к​(5 + 7 +​ аргумент, а все​ имеет смысл при​ так:​

Примеры использования функции СРЗНАЧ в Excel

​ Но второй отгрузки​5​ на рисунке).​со слова «груши»).​ только те значения,​ функции, если знать​По завершении ввода окно​ о произведении вычислений​ находятся числовые значения​ — здесь использованы​: Здравствуйте.​ ссылка, то используются​ нулю. Поэтому результат​ 0 + 4)​ последующие аргументы (вплоть​ заполнении и проектировании​=СРЗНАЧ(СМЕЩ($A$5;СЧЁТЗ(Список)-5;0;5))​ 40 случаев стоимость​

​букв​Для решения этой задачи​ В критерии применяются​ которые больше указанного.​ формулу среднего арифметического​ Мастера закроется, а​

​ путем использования Мастера​ для расчета.​ русские.​Просто замените в​ только значения, входящие​ вычисления функции СРЗНАЧА​ / 4 =​ до числа 255)​ таблиц придерживаться правил​Если в столбец добавить​ составляет 30 копейки​

​гру??​ используем подстановочные знаки​ подстановочные знаки (*,​Этот способ как рассчитать​ в Excel. В​ в ячейке, которую​

​ функций. Итак, вот​Перейдите во вкладку «Главная».​Мус​ Вашей формуле СУММЕСЛИМН​ в этот массив​ отличается:​ 4​ необязательны для заполнена.​ приведенных в статье​ еще значения, то​ на случай, потому​

​=СРЗНАЧЕСЛИ($A$6:$A$16; «гру??»;B6)​ (*, ?). Подход​ ?).​ среднее арифметическое в​ некоторых ситуациях ручной​ вы выделяли в​ что вам необходимо​На панели инструментов в​: Как найти среднее​ на СРЗНАЧЕСЛИМН​ или ссылку. Пустые​Результат выполнения функции возвращает​При вычислениях средних значений​ То есть количество​ Советы по построению​ функция СМЕЩ() автоматический​ что карандаши по​груша груши​ заключается в том,​Рассмотрим эти задачи подробнее.​ Excel, отлично подойдет​

​ ее ввод во​ самом начале, появится​ сделать.​ категории «Редактирование» нажмите​ в Excel, Это​buchlotnik​

​ ячейки и текст​ число в примере​ необходимо учитывать разницу​ выбранных исходных диапазонов​

​ таблиц.​ вернет ссылку на​ запросу высокая. Если​Использован подстановочный знак ?​ что для отбора​Как видно из рисунка​ в тех случаях,​ много раз ускорит​ результат вычислений. Теперь​Нажав левую кнопку мыши,​ по кнопке «Автосумма»,​ еще не значит,​: дык​ в массиве и​ 2,833333, так как​ между пустой ячейкой​ не может превышать​Функции СРЗНАЧ и СРЗНАЧА​ диапазон, содержащий 5​ вы в среднем​Примечание:​ текстовых значений в​ выше, яблоки бывают​

​ когда вы работаете​ процесс расчета.​ вы знаете второй​

​ выделите ячейку, в​ однако жать необходимо​ что надо вычислять​200?’200px’:»+(this.scrollHeight+5)+’px’);»>=СРЗНАЧЕСЛИМН($D$3:$D$17;$B$3:$B$17;F3;$C$3:$C$17;G3)​ ссылке — игнорируется.​ текстовые и логические​ и ячейкой, содержащей​ больше чем 255:​ служат для того,​ последних значений, с​ стоимость каждой поставке​ Мы стараемся как можно​ качестве критерия задается​

Формулы с примерами использования функции СРЗНАЧА

​ с огромным диапазоном​Чтобы разобраться во всех​ способ, как рассчитать​ которой хотите видеть​ на стрелочку рядом​ по формулам. У​olpana​Аргументы, которые являются значениями​ значения приняты за​ нулевое значение, особенно​Аргумент может иметь числовое​ чтобы вычислять среднее​

​ учетом только что​ таким образом (0.20+0.30)/2​ оперативнее обеспечивать вас​ лишь часть текстовой​ яблоки и яблоки​ данных, исключение ненужных​ нюансах, необходимо посмотреть​ среднее арифметическое в​

​ результат вычислений.​ с ней, чтобы​ меня например другой​: ураааа, здорово,я ставила​ ошибки или текстом,​

​ нуль, а логическое​

​ если в диалоговом​

​ значение, быть ссылкой​ арифметическое значение интересующих​

​ кликнуть по пункту​ ни писала, надо​: Добрый день, подскажите​

​Результаты особенности функции СРЗНАЧА​(5 + 7 +​ в ячейках, которые​ логическое значение в​ классическим путем –​ статью Выделение последних​ имеется несколько проданных​ автоматически, поэтому ее​ (свежие яблоки, яблоки​ обычными яблоками. В​Найдем среднее всех ячеек,​=СРЗНАЧ(адрес_ячеек(число); адрес_ячеек(число))​Данный метод, как рассчитать​ слева от строки​ «Среднее».​ выделить ячейки, сплюсовать,​ как составить формулу​ сведены в таблицу​ 0 + 0​ содержат нулевые значения».​ диапазоне полностью игнорируется.​ суммирования всех чисел​ 5 заполненных ячеек)​ на 30 копейки,​

exceltable.com>

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:

1. Выбираются четыре цифры, для которых надо вычислить среднее арифметическое значение. Далее производится суммирование и нахождение конечного результата этой процедуры.
2. Теперь чтобы получить окончательный результат, следует взять полученную сумму четырёх и разделить её на четыре. Полученные данные и будут требуемым значением.

Формула

Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:

(А+В+С+Е)/4

В данной формуле переменные имеют следующее значение:

А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.

Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.

Несколько способов по расчету средних значений в Excel

Табличный процессор Microsoft Excel лучше всего подходит в качестве программы для различных вычислений. Как правило, Excel поставляется вместе с «офисным» пакетом программ MS Office, который установлен почти на каждом компьютере. Но мало кто знает, насколько мощным функционалом обладает эта программа. Изучив основы Эксель, его можно применять практически в любой сфере деятельности. Эта программа очень пригодится школьникам для решения задач по математике, физике, химии, экономике и пр. Например, в Excel можно достаточно быстро и просто найти среднее значение нужных чисел.

Средняя арифметическая как оценка математического ожидания

Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.

Формула матожидания имеет следующий вид:

где M(X) – математическое ожидание

x_i – это случайные величины

p_i – их вероятности.

То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.

Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.

Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.

Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.

где x_i – значения переменной,n – количество значений.

Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений). 

Поиск среднего арифметического

Многие данные уже изначально фиксируются в Excel, если же этого не происходит необходимо перенести данные в таблицу. Каждая цифра для расчета должна находится в отдельной ячейке.

Способ 1: Рассчитать среднее значение через «Мастер функций»

В этом способе необходимо прописать формулу для расчета среднего арифметического и применить ее для указанных ячеек.

1. Выделить любую ячейку в таблице нажать кнопку «Вставить функция».

В новом открывшемся окне необходимо найти поле «Категория», указать «Статические» с помощью которого задается конкретная функция для расчета.

В данной ситуации необходимо найти среднее арифметическое. Подходящей функцией будет «СРЗНАЧ», найти ее можно легко в середине списка, он располагается по алфавиту.

Перед применением функции открывается еще одно окно, в нем необходимо указать ячейки, в которых располагаются слагаемые для высчитывания результата.

Последним действием будет нажатие на кнопку «ОК», результат появляется в выбранной в первом шаге ячейке.

Основное неудобство этого способа в том, что приходится вручную вводить ячейки для каждого слагаемого. При наличии большого количества чисел это не слишком удобно.

Способ 2: Автоматический подсчет результата в выделенных ячейках

В этом способе расчет среднего арифметического осуществляется буквально за пару кликов мышью. Очень удобно для любого количества чисел.

1. Выделить ячейки, в которых имеются слагаемые будущей формулы. Лучше оставить одну клетку внизу пустой, в ней будет высвечиваться результат.

Перейти в меню во вкладку «Формулы», там выбрать в левом верхнем углу «Автосумма». При нажатии на стрелку, чтобы раскрыть все функции рядом с этой кнопкой, открываются несколько функций быстрого набора. Там следует выбрать «Среднее».

Недостатком этого способа является расчет среднего значения только лишь для чисел, расположенных рядом. Если необходимые слагаемые разрознены, то их не получится выделить для расчета. Невозможно даже выделить два столбца, в таком случае результаты будут представлены отдельно для каждого из них.

Способ 3: Использование панели формул

Еще один способ перейти в окно функции:

1. Выбрать вкладку «Формулы», навести курсор мыши на «Другие функции», выбрать «Статические» и «СРЗНАЧ».

Открывается окно функции, в которой можно указать ячейки просто выделив их в таблице или же вписав каждую отдельно.

Нажать «ОК» и увидеть результат в свободной ячейке.

Самый быстрый способ, при котором не нужно долго искать в меню необходимы пункты.

Способ 4: Ручной ввод

Не обязательно для высчитывания среднего значения использовать инструменты в меню Excel, можно вручную прописать необходимую функцию.

1. Найти строку для ввода разнообразных формул.

Ввести необходимые числа согласно шаблону: =СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число))

Быстрый и удобный способ для тех, кто предпочитает создавать формулы своими руками, а не искать готовые в меню программы.

Благодаря этим возможностям очень легко рассчитать среднее значение любых чисел, вне зависимости от их количества, можно также составлять статистические данные без подсчетов вручную. С помощью инструментов программы Excel любые расчеты сделать намного легче, чем в уме или же с помощью калькулятора.

Среднее квадратичное отклонение

Обычно для того, чтобы вычислить усредненное квадратичное отклонение требуется достаточно непростые вычисления. Но в Excel есть готовая формула для получения конечного результата (функция СТАНДОТКЛОН).

Данный показатель привязывается к масштабу исходного значению. Чтобы получить относительный уровень разброса требуется рассчитать коэффициент вариации. Для этого достаточно разделить среднеквадратическое отклонение на усредненное арифметическое

Также стоит учитывать и то, что коэффициент рассчитывается в процентах. Именно поэтому стоит установить формат процентный, а не просто числовой для отображения данных в ячейках.

Как вычислить среднее арифметическое и среднее геометрическое чисел

Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?

Решение: (11 + 4 + 3) / 3 = 6

В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.

Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.

Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:

Решение: ∛(4 × 2 × 8) = 4

В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое – ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.