Midpointrounding перечисление

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Банковское округление (англ. banker’s rounding) — округление для этого случая происходит к ближайшему чётному, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике). Также часто используется округление с неравными вероятностями (вероятность округления вверх равна дробной части), этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным реккурентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Допустимы ли расчеты с работниками в полных рублях?

Начислениезаработной платы округлятьнельзя:

• размер тарифной ставки (оклад) в точной сумме должен быть указан в трудовом договоре (ст. 57 ТК РФ);
• все изменения в оплате труда подписываются двусторонним письменным соглашением (ст. 72 ТК РФ).

Если округлен расчет зарплаты – значит изменен

размер тарифной ставки (оклада) без согласования сторон, а этонарушение.Выплата заработной платы

можетокругляться в большую сторону в пользу работника (Письмо Минздравсоцразвития от 07.12.2005 N 4334-17):

• округление в меньшую сторону ведет к недоплате заработной платы;
• при окончательном расчете с работником (при увольнении) следует выплатить сумму в рублях и копейках;
• порядок округления (в большую сторону) при выплате зарплаты необходимо прописать ЛНА в соответствии со ст. 8 ТК РФ.

Пособия

по нетрудоспособности и в связи с материнством, а также пособия по уходу за ребенком округлятьнельзя (Письмо ФСС от 28.01.2014 N 17-03-11/06-1026).

Как округлить с помощью функции Excel?

А теперь перейдем непосредственно к практике. Что нужно делать, чтобы осуществить округление чисел с помощью функции? Для этого существует специальная функция ОКРУГЛ. Ее можно вызвать разными способами: через ленту в Excel 2007 версии и более новые.

Второй способ – написать вручную. Он более продвинутый, потому что нужно как минимум знать синтаксис.

Наиболее простой для новичка метод – воспользоваться мастером функций. Чтобы это сделать, нужно найти возле строки ввода формулы кнопочку, на которой написана комбинация маленьких буковок fx. Найти эту функцию можно в разделе «Математические», и после ее выбора будет предложено ввести аргументы. Каждый из них подписан, поэтому разобраться несложно.

Синтаксис функции ОКРУГЛ

Если используется ручной ввод, то нужно понимать, как правильно записывать формулу. Последовательность ввода значений называется синтаксисом. Любая функция имеет универсальный общий синтаксис. Сначала записывается знак равно, потом название функции, потом аргументы, которые прописываются в скобках, а разделяются между собой запятой. Количество аргументов может отличаться от функции к функции. В некоторых их вообще нет, а в ряде из них их хоть 5, хоть больше. 

В случае с функцией ОКРУГЛ их два. Давайте рассмотрим их более подробно.

Аргументы функции ОКРУГЛ

Итак, функция предусматривает два аргумента:

1. Число. Сюда указывается ссылка на ячейку. Или же можно ввести требуемое значение в этот аргумент вручную.

2. Количество знаков, на какое собираетесь осуществить округление.

Чтобы округлить целое число (то есть, которое не имеет ни одного знака после запятой), просто напишите знак минуса перед числом во втором параметре. Для округления до десятков, необходимо написать -1, до сотен – -2, и по такой логике далее. Чем больше модуль этого числа, тем на большее количество цифр будет осуществляться округление. 

Основы использования функции ОКРУГЛ

Давайте рассмотрим то как можно использовать эту функцию, на примере округления до тысяч.

Представим, у нас открылась такая таблица. Мы во вторую ячейку прописали формулу округления, и результат видим на этом скриншоте.

4

Возможно округление не только числа, но и любого значения. На примере это выглядит так. Представим, что у нас есть три столбца. В первом записывается цена товара, во втором – сколько его было куплено. Но и в третьем, соответственно, указывается итоговая стоимость. 

Представим, что наша задача – показывать сумму в рублях, а копейки игнорировать. Тогда получится следующая таблица.

5

По кратности

Excel дает возможность осуществлять округление чисел не до самого ближнего, а до того, которое является кратным по отношению к определенному. Для этого существует специальная функция, которая называется ОКРУГЛТ. С ее помощью можно добиться необходимой точности округления. 

Основных аргумента два. Первое – это непосредственно число, которое нужно округлить. Второй – это число, которому должно быть кратное заданное. Оба аргумента можно передавать как вручную, так и через ячейку. 

По количеству знаков

Все описанные выше примеры – это частные случаи округления по количеству знаков. Достаточно просто ввести в соответствующем аргументе функции необходимое количество знаков, которое нужно оставить. Собственно, это и все. 

Функции из библиотеки Math

Модуль необходим в Python. Он предоставляет пользователю широкий функционал работы с числами. Для обработки алгоритмов сначала проводят импорт модуля.

math.ceil

Функция преобразовывает значение в большую сторону (вверх). Этот термин применяется и в математике. Он означает число, которое равно или больше заданного.

Любая дробь находится между двумя целыми числами. Например, 2.3 лежит между 2 и 3. Функция ceil() определяет большую сторону и возводит к нему результат преобразования. Например:

Алгоритм определяет большую границу интервала с учетом знака:

math.floor

действует противоположно – округляет дробное значение до ближайшего целого, которое меньше или равно исходному. Округление происходит в меньшую сторону (вниз):

При округлении учитывается знак перед данными.

math.trunc

Функция характеризуется отбрасыванием дробной части. После преобразования получается целое значение без учета дроби. Такой алгоритм не является округлением в арифметическом смысле. В Пайтон просто игнорируется дробь независимо от ее значения:

Избавиться от дроби можно без подключения модуля. Для этого есть стандартная функция Она преобразовывает дробные числа в целые путем игнорирования дроби.

Дополнительные функции

Excel содержит и более специфические формулы, использование которых необходимо только в исключительных случаях.

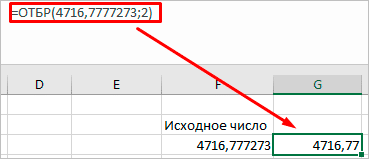
Например, функция ОТБР, которая отбрасывает числа от установленного разряда, то есть происходит не округление, а отсечение.

Функция ОКРВВЕРХ позволяет округлять значение ячейки до целого числа, при этом, если необходимо округлить в большую сторону кратно 100, необходимо указать точность 100, а если до 50, то, соответственно, 50.

Формула ОКРВНИЗ, аналогична предыдущей, только округляется вниз до целого. В зависимости от выбранной точности, можно округлить и до 5, однако это работает только для диапазона значений от 5,00 до 9,99.

Чтобы убрать округление, достаточно удалить из формулы любую из перечисленных функций, при этом исходное значения числа примет первоначальный вид.

Как видите, MS Excel обладает большим набором инструментов для работы с числами. Плюсом является то, что округление можно применять и к суммам, и к результатам вычисления выражений или функций. Описанные выше функции подойдут, как для бухгалтеров и людей, работающих с большими объемами чисел, так и для простых пользователей.

Эмпирические правила арифметики с округлениями

В тех случаях, когда нет необходимости в точном учёте вычислительных погрешностей, а требуется лишь приблизительно оценить количество точных цифр в результате расчёта по формуле, можно пользоваться набором простых правил округлённых вычислений:

Все исходные значения округляются до реальной точности измерений и записываются с соответствующим числом значащих цифр, так, чтобы в десятичной записи все цифры были надёжными (допускается, чтобы последняя цифра была сомнительной). При необходимости значения записываются со значащими правыми нулями, чтобы в записи указывалось реальное число надёжных знаков (например, если длина в 1 м реально измерена с точностью до сантиметров, записывается «1,00 м», чтобы было видно, что в записи надёжны два знака после запятой), или точность явно указывается (например, 2500±5 м — здесь надёжными являются только десятки, до них и следует округлять).
Промежуточные значения округляются с одной «запасной» цифрой.
При сложении и вычитании результат округляется до последнего десятичного знака наименее точного из параметров (например, при вычислении значения 1,00 м + 1,5 м + 0,075 м результат округляется до десятых метра, то есть до 2,6 м). При этом рекомендуется выполнять вычисления в таком порядке, чтобы избегать вычитания близких по величине чисел и производить действия над числами по возможности в порядке возрастания их модулей.
При умножении и делении результат округляется до наименьшего числа значащих цифр, которое имеют множители или делимое и делитель

Например, если тело при равномерном движении прошло дистанцию 2,5 × 103 метров за 635 секунд, то при вычислении скорости результат должен быть округлён до 3,9 м/с, поскольку одно из чисел (расстояние) известно лишь с точностью до двух значащих цифр.

Важное замечание: если один операндов при умножении или делитель при делении является по смыслу целым числом (то есть не результатом измерений непрерывной физической величины с точностью до целых единиц, а, например, количеством или просто целой константой), то количество значащих цифр в нём на точность результата операции не влияет, и оставляемое число цифр определяется только вторым операндом. Например, кинетическая энергия тела массой 0,325 кг, движущегося со скоростью 5,2 м/с, равна Ek=mv22=0.325⋅5.222=4.394≈4.4{\displaystyle E_{k}={\tfrac {mv^{2}}{2}}={\tfrac {0.325\cdot 5.2^{2}}{2}}=4.394\approx 4.4} Дж — округляется до двух знаков (по количеству значащих цифр в значении скорости), а не до одного (делитель 2 в формуле), так как значение 2 по смыслу — целая константа формулы, она является абсолютно точной и не влияет на точность вычислений (формально такой операнд можно считать «измеренным с бесконечным числом значащих цифр»).

При вычислении значения функции f(x){\displaystyle f\left(x\right)} требуется оценить значение модуля производной этой функции в окрестности точки вычисления

Если |f′(x)|⩽1{\displaystyle \left|f’\left(x\right)\right|\leqslant 1}, то результат функции точен до того же десятичного разряда, что и аргумент. В противном случае результат содержит меньше точных десятичных разрядов на величину log10⁡(|f′(x)|){\displaystyle \log _{10}\left(\left|f’\left(x\right)\right|\right)}, округлённую до целого в большую сторону.

Несмотря на нестрогость, приведённые правила достаточно хорошо работают на практике, в частности, из-за достаточно высокой вероятности взаимопогашения ошибок, которая при точном учёте погрешностей обычно не учитывается.

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление[источник не указан 145 дней] — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Округление до ближайшего чётного (в английском языке известно под названием англ. banker’s rounding — «округление банкира») — округление для этого случая происходит к ближайшему чётному числу, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике).
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным рекуррентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Примечания

1. ↑
2. Кнут Д. Э. Искусство программирования. Том 1. Основные алгоритмы = The Art of Computer Programming. Volume 1. Fundamental Algorithms / под ред. С. Г. Тригуб (гл. 1), Ю. Г. Гордиенко (гл. 2) и И. В. Красикова (разд. 2.5 и 2.6). — 3. — Москва: Вильямс, 2002. — Т. 1. — 720 с. — ISBN 5-8459-0080-8.
3. A’HEARN, B., J. BATEN AND D. CRAYEN (2009). “Quantifying Quantitative Literacy: Age Heaping and the History of Human Capital”, Journal of Economic History 69,783-808.
4. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. Техника вычислений и алгоритмизация: Вводный курс: Учебное пособие для студентов педагогических институтов по физико-математическим специальностям. — М: Просвещение, 1987. 160 с.: ил.
5. цит. по В. Гильде, З. Альтрихтер. «С микрокалькулятором в руках». Издание второе. Перевод с немецкого Ю. А. Данилова. М:Мир, 1987, стр. 64.

Интересный факт о strictfp

В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:

Создатели Java:

Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!

Создатели процессора Intel:

Ребята, мы улучшили наши процессоры, и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!

Ученые и все, кто занимается сверхточными расчетами:

Круто! Молодцы. Отличная новость.

Создатели Java:

Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.

Вот теперь все опять отлично! Не благодарите.

Ученые и все, кто занимается сверхточными расчетами:

Да вы там совсем охренели? Ану быстро вернули все как было!

Создатели Java:

Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!

Ученые и все, кто занимается сверхточными расчетами:

Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?

Создатели Java:

Гм. Что же вы сразу не сказали. Конечно, вернем.

Вернули возможность пользоваться всеми фичами крутых процессоров.

Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!

Поля

AwayFromZero	1	Режим округления до ближайшего числа. Когда число находится посредине между двумя другими числами, оно округляется до ближайшего к нулю числа.Round to nearest mode: when a number is halfway between two others, it is rounded toward the nearest number that is away from zero.
ToEven	Режим округления до ближайшего числа. Когда число находится посредине между двумя другими числами, оно округляется до ближайшего четного числа.Round to nearest mode: when a number is halfway between two others, it is rounded toward the nearest even number.
ToNegativeInfinity	3	Режим направленного округления. Число округляется в меньшую сторону до ближайшего результата, не большего, чем бесконечно точный результат.Directed mode: the number is rounded down, with the result closest to and no greater than the infinitely precise result.
ToPositiveInfinity	4	Режим направленного округления. Число округляется в большую сторону до ближайшего результата, не меньшего, чем бесконечно точный результат.Directed mode: the number is rounded up, with the result closest to and no less than the infinitely precise result.
ToZero	2	Режим направленного округления. Число округляется к нулю до ближайшего результата, не превышающего по порядку бесконечно точный результат.Directed mode: the number is rounded toward zero, with the result closest to and no greater in magnitude than the infinitely precise result.

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Округление десятичных чисел

Чтобы «обрезать» десятичное число, используются методы toFixed() или toPrecision(). Они оба принимают один аргумент, который определяет количество значимых и знаков после запятой, которые должны быть включены в результат:

• если для toFixed() аргумент не определен, значение по умолчанию равно , то есть без знаков после запятой; максимальное значение аргумента равно 20;
• если для toPrecision() аргумент не задан, число не изменяется.

var randNum = 6.25;
randNum.toFixed();
> "6"

Math.PI.toPrecision(1);
> "3"

var randNum = 87.335;
randNum.toFixed(2);
> "87.33"

var randNum = 87.337;
randNum.toPrecision(3);
> "87.3"

Примечание

И toFixed(), и toPrecision возвращают округленное строчное представление результата, а не число. Это означает, что прибавление rounded к randNum в результате даст конкатенацию строк, а не одно число:

console.log(randNum + rounded);
> "6.256"

Если нужно получить в результате JavaScript округление до сотых, используйте parseFloat():

var randNum = 6.25;
var rounded = parseFloat(randNum.toFixed(1));
console.log(rounded);
> 6.3

toFixed() и toPrecision() также являются полезными методами для усечения большого количества знаков после запятой. Это удобно при работе с числами, представляющими денежные единицы:

var wholeNum = 1
var dollarsCents = wholeNum.toFixed(2);
console.log(dollarsCents);
> "1.00"

Обратите внимание, что если в числе больше знаков, чем задано параметром точности, toPrecision будет выдавать результат в научном формате:

var num = 123.435
num.toPrecision(2);
> "1.2e+2"