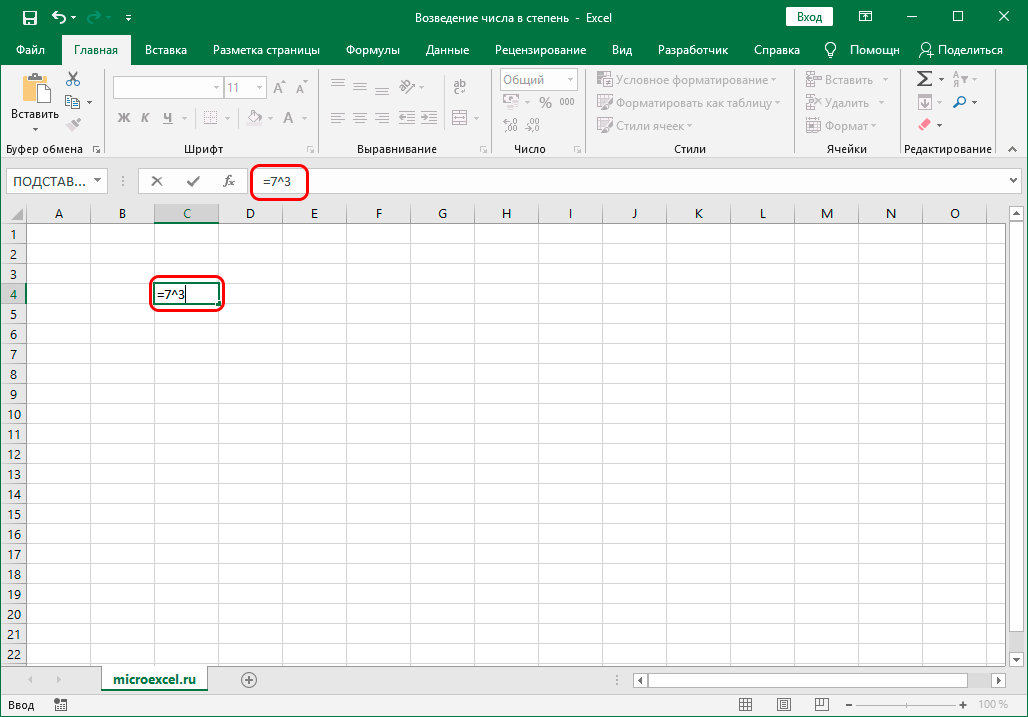
Как округлять числа

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Банковское округление (англ. banker’s rounding) — округление для этого случая происходит к ближайшему чётному, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике). Также часто используется округление с неравными вероятностями (вероятность округления вверх равна дробной части), этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным реккурентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Приближенные значения

В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.

У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин, иногда можно использовать приближенные значения.

Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.

Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.

Если длина платья 1м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.

Примерчики

Приближенное значение — число, которое получилось после округления.

Для записи результата округления используют знак «приблизительно равно» — ≈.

Округлить можно любое число — для всех чисел работают одни и те же правила.

Округлить число значит сократить его значение до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.

Чтобы ребенок решал задачки на округление легко и быстро, запишите его на уроки математики в онлайн-школу Skysmart. Ученики занимаются на интерактивной платформе, задают любые неловкие вопросы и гордятся своими успехами.

Эмпирические правила арифметики с округлениями

В тех случаях, когда нет необходимости в точном учёте вычислительных погрешностей, а требуется лишь приблизительно оценить количество точных цифр в результате расчёта по формуле, можно пользоваться набором простых правил округлённых вычислений:

Все исходные значения округляются до реальной точности измерений и записываются с соответствующим числом значащих цифр, так, чтобы в десятичной записи все цифры были надёжными (допускается, чтобы последняя цифра была сомнительной). При необходимости значения записываются со значащими правыми нулями, чтобы в записи указывалось реальное число надёжных знаков (например, если длина в 1 м реально измерена с точностью до сантиметров, записывается «1,00 м», чтобы было видно, что в записи надёжны два знака после запятой), или точность явно указывается (например, 2500±5 м — здесь надёжными являются только десятки, до них и следует округлять).
Промежуточные значения округляются с одной «запасной» цифрой.
При сложении и вычитании результат округляется до последнего десятичного знака наименее точного из параметров (например, при вычислении значения 1,00 м + 1,5 м + 0,075 м результат округляется до десятых метра, то есть до 2,6 м). При этом рекомендуется выполнять вычисления в таком порядке, чтобы избегать вычитания близких по величине чисел и производить действия над числами по возможности в порядке возрастания их модулей.
При умножении и делении результат округляется до наименьшего числа значащих цифр, которое имеют множители или делимое и делитель

Например, если тело при равномерном движении прошло дистанцию 2,5 × 103 метров за 635 секунд, то при вычислении скорости результат должен быть округлён до 3,9 м/с, поскольку одно из чисел (расстояние) известно лишь с точностью до двух значащих цифр.

Важное замечание: если один операндов при умножении или делитель при делении является по смыслу целым числом (то есть не результатом измерений непрерывной физической величины с точностью до целых единиц, а, например, количеством или просто целой константой), то количество значащих цифр в нём на точность результата операции не влияет, и оставляемое число цифр определяется только вторым операндом. Например, кинетическая энергия тела массой 0,325 кг, движущегося со скоростью 5,2 м/с, равна Ek=mv22=0.325⋅5.222=4.394≈4.4{\displaystyle E_{k}={\tfrac {mv^{2}}{2}}={\tfrac {0.325\cdot 5.2^{2}}{2}}=4.394\approx 4.4} Дж — округляется до двух знаков (по количеству значащих цифр в значении скорости), а не до одного (делитель 2 в формуле), так как значение 2 по смыслу — целая константа формулы, она является абсолютно точной и не влияет на точность вычислений (формально такой операнд можно считать «измеренным с бесконечным числом значащих цифр»).

При вычислении значения функции f(x){\displaystyle f\left(x\right)} требуется оценить значение модуля производной этой функции в окрестности точки вычисления

Если |f′(x)|⩽1{\displaystyle \left|f’\left(x\right)\right|\leqslant 1}, то результат функции точен до того же десятичного разряда, что и аргумент. В противном случае результат содержит меньше точных десятичных разрядов на величину log10⁡(|f′(x)|){\displaystyle \log _{10}\left(\left|f’\left(x\right)\right|\right)}, округлённую до целого в большую сторону.

Несмотря на нестрогость, приведённые правила достаточно хорошо работают на практике, в частности, из-за достаточно высокой вероятности взаимопогашения ошибок, которая при точном учёте погрешностей обычно не учитывается.

Способы округления чисел

Для округления чисел придумано много способов, они не лишены недостатков, однако часто используются для решения задач. Разберёмся в тонкостях каждого из них.

Если используется стандартная библиотека math, то в начале кода её необходимо подключить. Сделать это можно, например, с помощью инструкции: .

math.ceil() — округление чисел в большую сторону

Функция получила своё имя от термина «ceiling», который используется в математике для описания числа, которое больше или равно заданному.

Любая дробь находится в целочисленном интервале, например, 1.2 лежит между 1 и 2. Функция определяет, какая из границ интервала наибольшая и записывает её в результат округления.

Пример:

math.ceil(5.15) # = 6
math.ceil(6.666) # = 7
math.ceil(5) # = 5

Важно помнить, что функция определяет наибольшее число с учётом знака. То есть результатом округления числа -0.9 будет 0, а не -1.

math.floor() — округление чисел в меньшую сторону

Функция округляет дробное число до ближайшего целого, которое меньше или равно исходному. Работает аналогично функции , но с округлением в противоположную сторону.

Пример:

math.floor(7.9) # = 7
math.floor(9.999) # = 9
math.floor(-6.1) # = -7

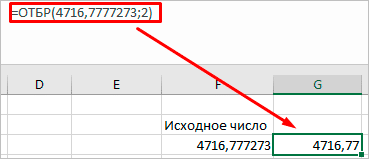
math.trunc() — отбрасывание дробной части

Возвращает целое число, не учитывая его дробную часть. То есть никакого округления не происходит, Python просто забывает о дробной части, приводя число к целочисленному виду.

Примеры:

math.trunc(5.51) # = 5
math.trunc(-6.99) # = -6

Избавиться от дробной части можно с помощью обычного преобразования числа к типу int. Такой способ полностью эквивалентен использованию .

Примеры:

int(5.51) # = 5
int(-6.99) # = -6

Нормальное округление

Python позволяет реализовать нормальное арифметическое округление, использовав функцию преобразования к типу int.

И хотя работает по другому алгоритму, результат её использования для положительных чисел полностью аналогичен выводу функции floor(), которая округляет числа «вниз». Для отрицательных аналогичен функции ceil().

Примеры:

math.floor(9.999) # = 9
int(9.999) # = 9
math.ceil(-9.999) # = -9
int(-9.999) # = -9

Чтобы с помощью функции int() округлить число по математическим правилам, необходимо добавить к нему 0.5, если оно положительное, и -0.5, если оно отрицательное.

Тогда операция принимает такой вид: int(num + (0.5 if num > 0 else -0.5)). Чтобы каждый раз не писать условие, удобно сделать отдельную функцию:

def int_r(num):
    num = int(num + (0.5 if num > 0 else -0.5))
    return num

Функция работает также, как стандартная функция округление во второй версии Python (арифметическое округление).

Примеры:

int_r(11.5) # = 12
int_r(11.4) # = 11
int_r(-0.991) # = -1
int_r(1.391) # = 1

round() — округление чисел

round() — стандартная функция округления в языке Python. Она не всегда работает так, как ожидается, а её алгоритм различается в разных версиях Python.

В Python 2

Во второй версии Python используется арифметическое округление. Оно обладает постоянно растущей погрешностью, что приводит к появлению неточностей и ошибок.

Увеличение погрешности вызвано неравным количеством цифр, определяющих, в какую сторону округлять. Всего 4 цифры на конце приводят к округлению «вниз», и 5 цифр к округлению «вверх».

Помимо этого, могут быть неточности, например, если округлить число 2.675 до второго знака, получится число 2.67 вместо 2.68. Это происходит из-за невозможности точно представить десятичные числа типа «float» в двоичном коде.

В Python 3

В третьей версии Python используется банковское округление. Это значит, что округление происходит до самого близкого чётного.

Такой подход не избавляет от ошибок полностью, но уменьшает шанс их возникновения и позволяет программисту добиться большей точности при вычислениях.

Примеры:

round(3.5) # = 4
round(9.5) # = 10
round(6.5) # = 6
round(-6.5) # = -6
round(-7.5) # = -8

Но если вам по каким то причинам нужно округление как в Python 2, то можно воспользоваться функцией написанной нами выше на основе приведения к целому числу.

Округление до сотых

У функции есть ещё один аргумент. Он показывает до какого количества знаков после запятой следует округлять. Таким образом, если нам надо в Python округлить до сотых, этому параметру следует задать значение 2.

Пример округления до нужного знака:

round(3.555, 2) # = 3.56
round(9.515,1) # = 9.5
round(6.657,2) # = 6.66

Выбор способа округления

Существует несколько способов округления в зависимости от способа применения результата: округление к меньшему/ большему, округление к меньшему/ большему по модулю, округление к ближайшему целому, округление к ближайшему чётному и т. д… Округление к ближайшему целому, в свою очередь, можно делать по-разному в зависимости от того, какой результат должен получиться, если дробная часть равна 0,5. Я буду рассматривать округление к ближайшему целому, причём 0,5 будет округляться в большую (по модулю) сторону.

Требования к корректной реализации Round() заключаются в следующем:

• правильно округляет до ближайшего целого все конечные числа;
• поддерживает специальные значения (NaN, Inf, -0), возвращая их без изменений.

Я буду использовать следующие тестовые примеры для проверки корректности, в каждой паре содержатся исходное значение и предполагаемый результат выполнения функции Round():

В этом списке есть обычные числа, специальные значения и некоторые граничные случаи, с которыми простым алгоритмам сложно справиться

Обратите внимание, что, поскольку мы используем float, мы не можем использовать число 0,49999999999999999 в качестве ближайшего к 0,5, так как из-за ограниченной точности float это число в точности равно 0,5. Вместо этого я использую 0,49999999999999994

Реализации, предложенные в закрытом тикете, явно не были проверены на подобных данных, часто не работали даже те из них, которые были предложены известными людьми. Это лишний раз доказывает, насколько сложно написать Round().

int(f + 0.5)

Первая реализация, предложенная rsc, выглядела следующим образом:

Она некорректно работает с особыми значениями, отрицательными числами, числами больше math.MaxInt64 и числами, близкими к 0,5:

Floor() or Ceil()

Второй предложенный вариант учитывал отрицательные числа:

однако продолжал некорректно работать в некоторых случаях:

Первые два теста не проходят, потому что результат разности n — 0,5 равен в точности -1,0, тогда как мы ожидаем получить что-то точно большее, чем -1,0. Если посмотреть на , можно понять, как решить эту проблему.

Самое интересное, что эта ошибка не является такой уж редкой. До версии 6 точно такая же присутствовала в Java. Хорошо, что с тех пор реализация улучшилась.

int и Copysign

В третьем предложении от minux была предпринята другая попытка решить проблему отрицательных чисел:

И этот вариант всё равно ломает тесты:

Как видно, часть тестов стала проходить, однако другие начали падать. Была предпринята попытка улучшить этот алгоритм:

Однако и она провалилась:

Этот вариант выглядит лучше остальных, но и он некорректно обрабатывает особые значения и большие числа. Первую проблему можно решить с помощью дополнительных условий, но со второй справиться не так просто.

Мы рассмотрели уже четыре варианта, и в каждом из них нашлись изъяны. Настало время посмотреть, как Round() реализуют авторы различных пакетов.

Kubernetes

Kubernetes 1.7 содержит реализацию:

Она ломает следующие тесты:

Судя по тому, что функция возвращает int32, она не предназначена для работы с большими числами. Однако она некорректно работает и с числами, которые близки к 0,5.

Использование округлений при работе с числами ограниченной точности

Реальные физические величины всегда измеряются с некоторой конечной точностью, которая зависит от приборов и методов измерения и оценивается максимальным относительным или абсолютным отклонением неизвестного истинного значения от измеренного, что в десятичном представлении значения соответствует либо определённому числу значащих цифр, либо определённой позиции в записи числа, все цифры после (правее) которой являются незначащими (лежат в пределах ошибки измерения). Сами измеренные параметры записываются с таким числом знаков, чтобы все цифры были надёжными, возможно, последняя — сомнительной. Погрешность при математических операциях с числами ограниченной точности сохраняется и изменяется по известным математическим законам, поэтому когда в дальнейших вычислениях возникают промежуточные значения и результаты с больши́м числом цифр, из этих цифр только часть являются значимыми. Остальные цифры, присутствуя в значениях, фактически не отражают никакой физической реальности и лишь отнимают время на вычисления. Вследствие этого промежуточные значения и результаты при вычислениях с ограниченной точностью округляют до того количества знаков, которое отражает реальную точность полученных значений. На практике обычно рекомендуется при длинных «цепочных» ручных вычислениях сохранять в промежуточных значениях на одну цифру больше. При использовании компьютера промежуточные округления в научно-технических приложениях чаще всего теряют смысл, и округляется только результат.

Так, например, если задана сила 5815 гс с точностью до грамма силы и длина плеча 1,4 м с точностью до сантиметра, то момент силы в кгс по формуле M=(mg)⋅h{\displaystyle M=(mg)\cdot h}, в случае формального расчёта со всеми знаками, окажется равным: 5,815 кгс • 1,4 м = 8,141 кгс•м. Однако если учесть погрешность измерения, то мы получим, что предельная относительная погрешность первого значения составляет 1/5815 ≈ 1,7•10−4, второго — 1/140 ≈ 7,1•10−3, относительная погрешность результата по правилу погрешности операции умножения (при умножении приближённых величин относительные погрешности складываются) составит 7,3•10−3, что соответствует максимальной абсолютной погрешности результата ±0,059 кгс•м! То есть в реальности, с учётом погрешности, результат может составлять от 8,082 до 8,200 кгс•м, таким образом, в рассчитанном значении 8,141 кгс•м полностью надёжной является только первая цифра, даже вторая — уже сомнительна! Корректным будет округление результата вычислений до первой сомнительной цифры, то есть до десятых: 8,1 кгс•м, или, при необходимости более точного указания рамок погрешности, представить его в виде, округлённом до одного-двух знаков после запятой с указанием погрешности: 8,14 ± 0,06 кгс•м.

Правила округления чисел

Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:

• Если цифра равняется или больше 5, то значащее значение округляют с увеличением на 1.
• Если цифра меньше 5, то значение округляют без увеличения.

Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.

Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.

Что мы узнали?

Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Зачем нужно округление

Округлять числа необходимо для точности измерений. В некоторых сферах жизни погрешности в расчетах могут иметь очень серьезные последствия. Для этого существует метрология — наука, изучающая правила округления чисел и погрешности.

Приведем несколько примеров, в которых неправильное округление не приведет ни к чему страшному:

Средняя зарплата в нашей стране. Очень интересный показатель, который постоянно меняется. Например, по данным за 2015 год, средняя зарплата составила 32560 рублей. Если выражать в тысячах, получится число 32,56. Согласно математическим правилам его можно округлить до 33. После чего вынести официальную версию, что средняя зарплата равна 33 тысячам рублей.
Стоимость покупки. В каждом супермаркете можно увидеть товар со стоимостью, например, 48 рублей и 60 копеек. Если вы хотите совершить много покупок, логично будет прибавить к общей сумме 49 или даже 50 рублей. Это избавит вас от неловких ситуаций, когда вам не хватает совсем немного для оплаты покупки. А также сохранит вам лишнюю мелочь, которая может пригодиться потом.
Показания весов, как правило, ошибаются на 0,5—1 процент. Соответственно, если вы встали на весы, и они показали 50 килограммов, значит, вы можете весить на 500 граммов больше или меньше, чем увидели на шкале прибора. Согласитесь, ничего страшного в этом нет. Главное, что вы узнали свой примерный вес

Важно понять, что в мире все приблизительно, и везде есть погрешности.
Средний балл — самая распространённая ситуация. Например, для поступления в университет на бюджетное место необходим средний балл аттестата выше, чем 4,5

Абитуриента не примут, если его средний балл равен 4,48. По математическим правилам 4,48 можно округлить до четырёх с половиной. Однако в жизни такие правила не всегда работают.

Однако есть ситуации, где правильное округление является необходимостью. Наверняка читатель мог подумать, зачем нужна какая-то наука об округлении? Ведь все просто — округлять можно как в большую, так и в меньшую сторону, в зависимости от личной выгоды. Такой принцип применим не ко всем сферам жизни. Науку об округлении в первую очередь необходимо изучать инженерам-электроникам.

Люди, которые учились в технических институтах, знают, что при разработке определенных приборов необходимо провести много различных расчетов. Чаще всего промежуточными результатами этих расчетов являются нецелые числа. Чтобы они не повлияли на конечный результат, их нужно округлять только по определённым правилам либо вообще этого не делать, а работать с конечным результатом.

Суть в том, что погрешность может быть довольно велика (около 5 процентов), и это может плохо кончиться. Например, посчитанное значение напряжения тока в электрической цепи может быть неподходящим, и техническое устройство работать не будет. Или того хуже, инженера может ударить током.

Чтобы избежать подобных казусов, студентам технических вузов и инженерам необходимо знать правила округления.

Как округлить с помощью функции Excel?

А теперь перейдем непосредственно к практике. Что нужно делать, чтобы осуществить округление чисел с помощью функции? Для этого существует специальная функция ОКРУГЛ. Ее можно вызвать разными способами: через ленту в Excel 2007 версии и более новые.

Второй способ – написать вручную. Он более продвинутый, потому что нужно как минимум знать синтаксис.

Наиболее простой для новичка метод – воспользоваться мастером функций. Чтобы это сделать, нужно найти возле строки ввода формулы кнопочку, на которой написана комбинация маленьких буковок fx. Найти эту функцию можно в разделе «Математические», и после ее выбора будет предложено ввести аргументы. Каждый из них подписан, поэтому разобраться несложно.

Синтаксис функции ОКРУГЛ

Если используется ручной ввод, то нужно понимать, как правильно записывать формулу. Последовательность ввода значений называется синтаксисом. Любая функция имеет универсальный общий синтаксис. Сначала записывается знак равно, потом название функции, потом аргументы, которые прописываются в скобках, а разделяются между собой запятой. Количество аргументов может отличаться от функции к функции. В некоторых их вообще нет, а в ряде из них их хоть 5, хоть больше. 

В случае с функцией ОКРУГЛ их два. Давайте рассмотрим их более подробно.

Аргументы функции ОКРУГЛ

Итак, функция предусматривает два аргумента:

1. Число. Сюда указывается ссылка на ячейку. Или же можно ввести требуемое значение в этот аргумент вручную.

2. Количество знаков, на какое собираетесь осуществить округление.

Чтобы округлить целое число (то есть, которое не имеет ни одного знака после запятой), просто напишите знак минуса перед числом во втором параметре. Для округления до десятков, необходимо написать -1, до сотен – -2, и по такой логике далее. Чем больше модуль этого числа, тем на большее количество цифр будет осуществляться округление. 

Основы использования функции ОКРУГЛ

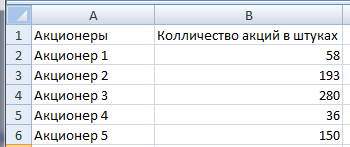
Давайте рассмотрим то как можно использовать эту функцию, на примере округления до тысяч.

Представим, у нас открылась такая таблица. Мы во вторую ячейку прописали формулу округления, и результат видим на этом скриншоте.

4

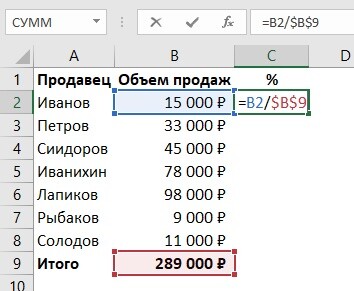
Возможно округление не только числа, но и любого значения. На примере это выглядит так. Представим, что у нас есть три столбца. В первом записывается цена товара, во втором – сколько его было куплено. Но и в третьем, соответственно, указывается итоговая стоимость. 

Представим, что наша задача – показывать сумму в рублях, а копейки игнорировать. Тогда получится следующая таблица.

5

По кратности

Excel дает возможность осуществлять округление чисел не до самого ближнего, а до того, которое является кратным по отношению к определенному. Для этого существует специальная функция, которая называется ОКРУГЛТ. С ее помощью можно добиться необходимой точности округления. 

Основных аргумента два. Первое – это непосредственно число, которое нужно округлить. Второй – это число, которому должно быть кратное заданное. Оба аргумента можно передавать как вручную, так и через ячейку. 

По количеству знаков

Все описанные выше примеры – это частные случаи округления по количеству знаков. Достаточно просто ввести в соответствующем аргументе функции необходимое количество знаков, которое нужно оставить. Собственно, это и все. 

Получение приближенных значений

Это математическое действие осуществляется по определенным правилам.

Но для каждого множества чисел они разные. Отмечают, что округлить можно целые числа и десятичные дроби.

А вот с обыкновенными дробями действие не выполняется.

Сначала их необходимо перевести в десятичные дроби, а затем приступить к процедуре в необходимом контексте.

Правила приближения значений заключаются в следующем:

• для целых – замена разрядов, следующих за округляемым, нулями,
• для десятичных дробей – отбрасывания всех чисел, которые находятся за округляемым разрядом.

К примеру, округляя 303 434 до тысяч, необходимо заменить сотни, десятки и единицы нулями, то есть 303 000. В десятичных дробях 3,3333 округляя до десятых, просто отбрасывают все последующие цифры и получают результат 3,3.