Math.round()

Trigonometry functions #

Function	Description
math.acos(x)	Calculate the inverse cosine of a value.
math.acosh(x)	Calculate the hyperbolic arccos of a value, defined as .
math.acot(x)	Calculate the inverse cotangent of a value, defined as .
math.acoth(x)	Calculate the hyperbolic arccotangent of a value, defined as .
math.acsc(x)	Calculate the inverse cosecant of a value, defined as .
math.acsch(x)	Calculate the hyperbolic arccosecant of a value, defined as .
math.asec(x)	Calculate the inverse secant of a value.
math.asech(x)	Calculate the hyperbolic arcsecant of a value, defined as .
math.asin(x)	Calculate the inverse sine of a value.
math.asinh(x)	Calculate the hyperbolic arcsine of a value, defined as .
math.atan(x)	Calculate the inverse tangent of a value.
math.atan2(y, x)	Calculate the inverse tangent function with two arguments, y/x.
math.atanh(x)	Calculate the hyperbolic arctangent of a value, defined as .
math.cos(x)	Calculate the cosine of a value.
math.cosh(x)	Calculate the hyperbolic cosine of a value, defined as .
math.cot(x)	Calculate the cotangent of a value.
math.coth(x)	Calculate the hyperbolic cotangent of a value, defined as .
math.csc(x)	Calculate the cosecant of a value, defined as .
math.csch(x)	Calculate the hyperbolic cosecant of a value, defined as .
math.sec(x)	Calculate the secant of a value, defined as .
math.sech(x)	Calculate the hyperbolic secant of a value, defined as .
math.sin(x)	Calculate the sine of a value.
math.sinh(x)	Calculate the hyperbolic sine of a value, defined as .
math.tan(x)	Calculate the tangent of a value.
math.tanh(x)	Calculate the hyperbolic tangent of a value, defined as .

Способы записи числа

Представьте, что нам надо записать число 1 миллиард. Самый очевидный путь:

Но в реальной жизни мы обычно опускаем запись множества нулей, так как можно легко ошибиться. Укороченная запись может выглядеть как или для 7 миллиардов 300 миллионов. Такой принцип работает для всех больших чисел.

В JavaScript можно использовать букву , чтобы укоротить запись числа. Она добавляется к числу и заменяет указанное количество нулей:

Другими словами, производит операцию умножения числа на 1 с указанным количеством нулей.

Сейчас давайте запишем что-нибудь очень маленькое. К примеру, 1 микросекунду (одна миллионная секунды):

Записать микросекунду в укороченном виде нам поможет .

Если мы подсчитаем количество нулей , их будет 6. Естественно, верная запись .

Другими словами, отрицательное число после подразумевает деление на 1 с указанным количеством нулей:

Шестнадцатеричные числа широко используются в JavaScript для представления цветов, кодировки символов и многого другого. Естественно, есть короткий стиль записи: , после которого указывается число.

Например:

Не так часто используются двоичные и восьмеричные числа, но они также поддерживаются для двоичных и для восьмеричных:

Есть только 3 системы счисления с такой поддержкой. Для других систем счисления мы рекомендуем использовать функцию (рассмотрим позже в этой главе).

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Банковское округление (англ. banker’s rounding) — округление для этого случая происходит к ближайшему чётному, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике). Также часто используется округление с неравными вероятностями (вероятность округления вверх равна дробной части), этот способ делает накопление ошибок случайной величиной с нулевым математическим ожиданием.
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным реккурентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Why Round Numbers?

You may be wondering why anybody would want to go from having values
that are more precise to having values that are less precise. In this
section, we are going to look at some examples.

Displaying on the Pixel

Whenever you are doing anything on the canvas or positioning DOM elements using code, you’ll be doing a whole lot of pixel pushing to the screen. The things you are drawing on screen look best when its position and size values fall on a whole pixel. If you are using
fractional values, what you are displaying may end up looking blurry:

An easy way to ensure everything falls on pixel boundaries is to
round any position or size value to a whole number.

Improving Performance

Working with round numbers is faster
than having to deal with numbers that contain extra precision. Nuff said about that 😛

Dealing with JavaScript’s Quirky Number Handling

JavaScript stores all numbers internally as floating point values.
This means your calculations could be subject to floating point
shenanigans. Here is an example:

var blah = 0.2 * 0.4;

What do you think the value of blah actually is? If you guessed .08,
you would be wrong. Here is what actually shows up:

There is a reason why the 2 awkwardly shows up at the end of the result. It has to do with how
fractions are represented as floating point values. It is weird, but
that’s just how it is. By rounding your number, you can account for the unnecessary
precision and just get .08 like you probably wanted all along.

Методы

В разных сферах могут применяться различные методы округления. Во всех этих методах «лишние» знаки обнуляют (отбрасывают), а предшествующий им знак корректируется по какому-либо правилу.

• Округление к ближайшему целому (англ. rounding) — наиболее часто используемое округление, при котором число округляется до целого, модуль разности с которым у этого числа минимален. В общем случае, когда число в десятичной системе округляют до N-го знака, правило может быть сформулировано следующим образом:
  • если N+1 знак < 5, то N-й знак сохраняют, а N+1 и все последующие обнуляют;
  • если N+1 знак ≥ 5, то N-й знак увеличивают на единицу, а N+1 и все последующие обнуляют;

  Например: 11,9 → 12; −0,9 → −1; −1,1 → −1; 2,5 → 3.

  Максимальная дополнительная абсолютная погрешность, вносимая при таком округлении (погрешность округления), составляет ±0,5 последнего сохраняемого разряда.

• Округление к меньшему по модулю (округление к нулю, целое англ. fix, truncate, integer) — самое «простое» округление, поскольку после обнуления «лишних» знаков предшествующий знак сохраняют, то есть технически оно состоит в отбрасывании лишних знаков. Например, 11,9 → 11; −0,9 → 0; −1,1 → −1). При таком округлении может вноситься погрешность в пределах единицы последнего сохраняемого разряда, причём в положительной части числовой оси погрешность всегда отрицательна, а в отрицательной — положительна.
• Округление к большему (округление к +∞, округление вверх, англ. ceiling — досл. «потолок») — если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу, если число положительное, или сохраняют, если число отрицательное. В экономическом жаргоне — округление в пользу продавца, кредитора (лица, получающего деньги). В частности, 2,6 → 3, −2,6 → −2. Погрешность округления — в пределах +1 последнего сохраняемого разряда.
• Округление к меньшему (округление к −∞, округление вниз, англ. floor — досл. «пол») — если обнуляемые знаки не равны нулю, предшествующий знак сохраняют, если число положительное, или увеличивают на единицу, если число отрицательное. В экономическом жаргоне — округление в пользу покупателя, дебитора (лица, отдающего деньги). Здесь 2,6 → 2, −2,6 → −3. Погрешность округления — в пределах −1 последнего сохраняемого разряда.
• Округление к большему по модулю (округление к бесконечности, округление от нуля) — относительно редко используемая форма округления. Если обнуляемые знаки не равны нулю, предшествующий знак увеличивают на единицу. Погрешность округления составляет +1 последнего разряда для положительных и −1 последнего разряда для отрицательных чисел.

Еще немного методов

В JavaScript также есть и другие 2 метода, которые занимаются округлением числовых представлений. Однако они несколько отличаются.

Речь пойдет о таких инструментах, как toFixed ()
и toPrecision ()
. Они отвечают не просто за округление, а за ее точность до определенных знаков. Давайте покопаем глубже.

toFixed ()

С помощью данного механизма можно указывать, до скольких знаков после запятой нужно округлить значение. Метод возвращает результат в виде строки. Ниже я прикрепил вариант с тремя разными вариантами. Проанализируйте полученные ответы.

Как видно, если не указать аргумента, то toFixed ()) округлит дробное значение до целого
числа. В третьей строке выполнено округление до 2-знаков,
а в четвертой – из-за параметра «7» было дописано еще три 0.

toPrecision ()

Данный метод действует несколько иначе. На месте аргумента можно оставить как пустое место, так и установить параметр. Однако последний будет округлять числа до указанного количества цифр, не обращая внимания на запятую. Вот какие результаты выдала программа, переписанная с прошлого примера:

Как явно преобразовать строку в число

Явно привести строку в число можно посредством следующих способов:

1. Использовать унарный оператор +, который необходимо поместить перед значением.

+'7.35';   // 7.35
+'текст';  // NaN

Этот способ пренебрегает пробелами в начале и конце строки, а также (переводом строки).

+' 7.35 ';    //7.35
+'7.35 \n ';  //7.35

Используя данный способ необходимо обратить внимание на то, что пустая строка или строка, состоящая из пробелов и , переводится в число 0. Кроме этого она также преобразует тип данных и логические значения к числу

+null;   //0
+true;   //1
+false;  //0
+'   ';  //0

2. Функция parseInt. Данная функция предназначена для преобразования аргумента в целое число. В отличие от использования унарного оператора +, данный метод позволяет преобразовать строку в число, в которой не все символы являются цифровыми. Начинает она преобразовывать строку, начиная с первого символа. И как только она встречает символ, не являющийся цифровым, данная функция останавливает свою работу и возвращает полученное число.

parseInt('18px');   //18
parseInt('33.3%');  //33

Данная функция может работать с разными системами счисления (двоичной, восьмеричной, десятичной, шестнадцатеричной). Указание основание системы счисления осуществляется посредством 2 аргумента.

Кроме этого рекомендуется, всегда указывать основание системы счисления и не полагаться на значение по умолчанию установленное этой функции, например в том или ином браузере.

parseInt('18px', 10);   //18
parseInt('33.3%', 10);  //33
parseInt('101',2);      //5
parseInt('B5',16);      //181

Кроме функции parseInt в JavaScript имеется метод Number.parseInt. Данный метод ничем не отличается от функции parseInt и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

3. Функция parseFloat. Функция parseFloat аналогична parseInt, за исключением того что позволяет выполнить преобразование аргумента в дробное число.

parseFloat('33.3%');  //33.3

Кроме этого функция parseFloat в отличие от parseInt не имеет 2 аргумента, и следовательно она всегда пытается рассмотреть строку как число в десятичной системе счисления.

parseFloat("3.14");
parseFloat("314e-2");
parseFloat("0.0314E+2");

Кроме функции parseFloat в JavaScript имеется метод Number.parseFloat. Данный метод ничем не отличается от функции parseFloat и был введён в JavaScript со спецификацией ECMASCRIPT 2015 (6).

Интересный факт о strictfp

В Java есть специальное ключевое слово (strict floating point), которого нет в других языках программирования. И знаете, зачем оно нужно? Оно ухудшает точность работы с вещественными числами. История его появления примерно такова:

Создатели Java:

Мы очень хотим, чтобы Java была суперпопулярна, и программы на Java выполнялись на как можно большем количестве устройств. Поэтому мы прописали в спецификацию Java-машины, что на всех типах устройств все программы должны выполняться одинаково!

Создатели процессора Intel:

Ребята, мы улучшили наши процессоры, и теперь все вещественные числа внутри процессора будет представлены не 8-ю, а 10-ю байтами. Больше байт — больше знаковых цифр. А это значит что? Правильно: теперь ваши научные вычисления будут еще более точными!

Ученые и все, кто занимается сверхточными расчетами:

Круто! Молодцы. Отличная новость.

Создатели Java:

Не-не-не, ребята. Мы же сказали: все Java-программы должны выполняться одинаково на всех устройствах. Принудительно выключаем возможность использования 10 байтовых вещественных чисел внутри процессоров Intel.

Вот теперь все опять отлично! Не благодарите.

Ученые и все, кто занимается сверхточными расчетами:

Да вы там совсем охренели? Ану быстро вернули все как было!

Создатели Java:

Ребята, это для вашей же пользы! Только представьте: все Java-программы выполняются одинаково на всех устройствах. Ну круто же!

Ученые и все, кто занимается сверхточными расчетами:

Нет. Совсем не круто. Быстро вернули все обратно! Или мы вашу Java вам знаете куда засунем?

Создатели Java:

Гм. Что же вы сразу не сказали. Конечно, вернем.

Вернули возможность пользоваться всеми фичами крутых процессоров.

Кстати. Мы так же специально добавили в язык слово : если его написать перед именем функции, вся работа с вещественными числами внутри этой функции будет одинаково плохой на всех устройствах!

Arithmetic functions #

Function	Description
math.abs(x)	Calculate the absolute value of a number.
math.add(x, y)	Add two or more values, .
math.cbrt(x )	Calculate the cubic root of a value.
math.ceil(x)	Round a value towards plus infinity If is complex, both real and imaginary part are rounded towards plus infinity.
math.cube(x)	Compute the cube of a value, .
math.divide(x, y)	Divide two values, .
math.dotDivide(x, y)	Divide two matrices element wise.
math.dotMultiply(x, y)	Multiply two matrices element wise.
math.dotPow(x, y)	Calculates the power of x to y element wise.
math.exp(x)	Calculate the exponent of a value.
math.expm1(x)	Calculate the value of subtracting 1 from the exponential value.
math.fix(x)	Round a value towards zero.
math.floor(x)	Round a value towards minus infinity.
math.gcd(a, b)	Calculate the greatest common divisor for two or more values or arrays.
math.hypot(a, b, …)	Calculate the hypotenusa of a list with values.
math.lcm(a, b)	Calculate the least common multiple for two or more values or arrays.
math.log(x )	Calculate the logarithm of a value.
math.log10(x)	Calculate the 10-base logarithm of a value.
math.log1p(x)	Calculate the logarithm of a .
math.log2(x)	Calculate the 2-base of a value.
math.mod(x, y)	Calculates the modulus, the remainder of an integer division.
math.multiply(x, y)	Multiply two or more values, .
math.norm(x )	Calculate the norm of a number, vector or matrix.
math.nthRoot(a)	Calculate the nth root of a value.
math.nthRoots(x)	Calculate the nth roots of a value.
math.pow(x, y)	Calculates the power of x to y, .
math.round(x )	Round a value towards the nearest integer.
math.sign(x)	Compute the sign of a value.
math.sqrt(x)	Calculate the square root of a value.
math.square(x)	Compute the square of a value, .
math.subtract(x, y)	Subtract two values, .
math.unaryMinus(x)	Inverse the sign of a value, apply a unary minus operation.
math.unaryPlus(x)	Unary plus operation.
math.xgcd(a, b)	Calculate the extended greatest common divisor for two values.

Неточные вычисления

Внутри JavaScript число представлено в виде 64-битного формата IEEE-754. Для хранения числа используется 64 бита: 52 из них используется для хранения цифр, 11 из них для хранения положения десятичной точки (если число целое, то хранится 0), и один бит отведён на хранение знака.

Если число слишком большое, оно переполнит 64-битное хранилище, JavaScript вернёт бесконечность:

Наиболее часто встречающаяся ошибка при работе с числами в JavaScript – это потеря точности.

Посмотрите на это (неверное!) сравнение:

Да-да, сумма и не равна .

Странно! Что тогда, если не ?

Но почему это происходит?

Число хранится в памяти в бинарной форме, как последовательность бит – единиц и нулей. Но дроби, такие как , , которые выглядят довольно просто в десятичной системе счисления, на самом деле являются бесконечной дробью в двоичной форме.

Другими словами, что такое ? Это единица делённая на десять — , одна десятая. В десятичной системе счисления такие числа легко представимы, по сравнению с одной третьей: , которая становится бесконечной дробью .

Деление на гарантированно хорошо работает в десятичной системе, но деление на – нет. По той же причине и в двоичной системе счисления, деление на обязательно сработает, а становится бесконечной дробью.

В JavaScript нет возможности для хранения точных значений 0.1 или 0.2, используя двоичную систему, точно также, как нет возможности хранить одну третью в десятичной системе счисления.

Числовой формат IEEE-754 решает эту проблему путём округления до ближайшего возможного числа. Правила округления обычно не позволяют нам увидеть эту «крошечную потерю точности», но она существует.

Пример:

И когда мы суммируем 2 числа, их «неточности» тоже суммируются.

Вот почему – это не совсем .

Не только в JavaScript

Справедливости ради заметим, что ошибка в точности вычислений для чисел с плавающей точкой сохраняется в любом другом языке, где используется формат IEEE 754, включая PHP, Java, C, Perl, Ruby.

Можно ли обойти проблему? Конечно, наиболее надёжный способ — это округлить результат используя метод toFixed(n):

Также можно временно умножить число на 100 (или на большее), чтобы привести его к целому, выполнить математические действия, а после разделить обратно. Суммируя целые числа, мы уменьшаем погрешность, но она все равно появляется при финальном делении:

Таким образом, метод умножения/деления уменьшает погрешность, но полностью её не решает.

Забавный пример

Попробуйте выполнить его:

Причина та же – потеря точности. Из 64 бит, отведённых на число, сами цифры числа занимают до 52 бит, остальные 11 бит хранят позицию десятичной точки и один бит – знак. Так что если 52 бит не хватает на цифры, то при записи пропадут младшие разряды.

Интерпретатор не выдаст ошибку, но в результате получится «не совсем то число», что мы и видим в примере выше. Как говорится: «как смог, так записал».

Два нуля

Другим забавным следствием внутреннего представления чисел является наличие двух нулей: и .

Все потому, что знак представлен отдельным битом, так что, любое число может быть положительным и отрицательным, включая нуль.

В большинстве случаев это поведение незаметно, так как операторы в JavaScript воспринимают их одинаковыми.

Algebra functions #

Function	Description
derivative(expr, variable)	Takes the derivative of an expression expressed in parser Nodes.
math.lsolve(L, b)	Finds one solution of a linear equation system by forwards substitution.
math.lsolveAll(L, b)	Finds all solutions of a linear equation system by forwards substitution.
math.lup(A)	Calculate the Matrix LU decomposition with partial pivoting.
math.lusolve(A, b)	Solves the linear system where is an matrix and is a column vector.
math.qr(A)	Calculate the Matrix QR decomposition.
rationalize(expr)	Transform a rationalizable expression in a rational fraction.
simplify(expr)	Simplify an expression tree.
math.slu(A, order, threshold)	Calculate the Sparse Matrix LU decomposition with full pivoting.
math.usolve(U, b)	Finds one solution of a linear equation system by backward substitution.
math.usolveAll(U, b)	Finds all solutions of a linear equation system by backward substitution.

Округление

Одна из часто используемых операций при работе с числами – это округление.

В JavaScript есть несколько встроенных функций для работы с округлением:

Округление в меньшую сторону: становится , а — .

Округление в большую сторону: становится , а — .

Округление до ближайшего целого: становится , — , а — .

(не поддерживается в Internet Explorer)

Производит удаление дробной части без округления: становится , а — .

Ниже представлена таблица с различиями между функциями округления:

Эти функции охватывают все возможные способы обработки десятичной части. Что если нам надо округлить число до количества цифр в дробной части?

Например, у нас есть и мы хотим округлить число до 2-х знаков после запятой, оставить только .

Есть два пути решения:

Умножить и разделить.
Например, чтобы округлить число до второго знака после запятой, мы можем умножить число на , вызвать функцию округления и разделить обратно.

Метод toFixed(n) округляет число до знаков после запятой и возвращает строковое представление результата.

Округляет значение до ближайшего числа, как в большую, так и в меньшую сторону, аналогично методу :

Обратите внимание, что результатом является строка. Если десятичная часть короче, чем необходима, будут добавлены нули в конец строки:

Мы можем преобразовать полученное значение в число, используя унарный оператор или , пример с унарным оператором: .

Выбор способа округления

Существует несколько способов округления в зависимости от способа применения результата: округление к меньшему/ большему, округление к меньшему/ большему по модулю, округление к ближайшему целому, округление к ближайшему чётному и т. д… Округление к ближайшему целому, в свою очередь, можно делать по-разному в зависимости от того, какой результат должен получиться, если дробная часть равна 0,5. Я буду рассматривать округление к ближайшему целому, причём 0,5 будет округляться в большую (по модулю) сторону.

Требования к корректной реализации Round() заключаются в следующем:

• правильно округляет до ближайшего целого все конечные числа;
• поддерживает специальные значения (NaN, Inf, -0), возвращая их без изменений.

Я буду использовать следующие тестовые примеры для проверки корректности, в каждой паре содержатся исходное значение и предполагаемый результат выполнения функции Round():

В этом списке есть обычные числа, специальные значения и некоторые граничные случаи, с которыми простым алгоритмам сложно справиться

Обратите внимание, что, поскольку мы используем float, мы не можем использовать число 0,49999999999999999 в качестве ближайшего к 0,5, так как из-за ограниченной точности float это число в точности равно 0,5. Вместо этого я использую 0,49999999999999994

Реализации, предложенные в закрытом тикете, явно не были проверены на подобных данных, часто не работали даже те из них, которые были предложены известными людьми. Это лишний раз доказывает, насколько сложно написать Round().

int(f + 0.5)

Первая реализация, предложенная rsc, выглядела следующим образом:

Она некорректно работает с особыми значениями, отрицательными числами, числами больше math.MaxInt64 и числами, близкими к 0,5:

Floor() or Ceil()

Второй предложенный вариант учитывал отрицательные числа:

однако продолжал некорректно работать в некоторых случаях:

Первые два теста не проходят, потому что результат разности n — 0,5 равен в точности -1,0, тогда как мы ожидаем получить что-то точно большее, чем -1,0. Если посмотреть на , можно понять, как решить эту проблему.

Самое интересное, что эта ошибка не является такой уж редкой. До версии 6 точно такая же присутствовала в Java. Хорошо, что с тех пор реализация улучшилась.

int и Copysign

В третьем предложении от minux была предпринята другая попытка решить проблему отрицательных чисел:

И этот вариант всё равно ломает тесты:

Как видно, часть тестов стала проходить, однако другие начали падать. Была предпринята попытка улучшить этот алгоритм:

Однако и она провалилась:

Этот вариант выглядит лучше остальных, но и он некорректно обрабатывает особые значения и большие числа. Первую проблему можно решить с помощью дополнительных условий, но со второй справиться не так просто.

Мы рассмотрели уже четыре варианта, и в каждом из них нашлись изъяны. Настало время посмотреть, как Round() реализуют авторы различных пакетов.

Kubernetes

Kubernetes 1.7 содержит реализацию:

Она ломает следующие тесты:

Судя по тому, что функция возвращает int32, она не предназначена для работы с большими числами. Однако она некорректно работает и с числами, которые близки к 0,5.

Round() в Go 1.10

Для тех, кто не знаком с устройством float (я в их числе), этот код выглядит совершенно непонятно. Попробуем разобраться, что же он делает:

Похоже, что мы берём битовое представление числа, сдвигаем его и применяем маску. Согласно :

Рассматривая приведённые выше константы, мы видим, что сдвиг составляет 64 — 11 — 1, что означает 64 бита на число, 11 из которых используются для показателя степени, один — для знака и 52 оставшихся бита — для мантиссы. Это означает, что используемый сдвиг удаляет биты мантиссы, а маска удаляет бит знака, оставляя нас только с показателем степени.

В полученном числе показатель степени записан не как он есть, а с прибавлением числа 1023 (это делается для того чтобы записывать отрицательные показатели для очень маленьких чисел), что означает, что мы должны вычесть 1023 из e, вычисленного выше, чтобы получить фактический показатель. Иными словами, если e < bias, то мы имеем отрицательный показатель степени, что означает, что абсолютное значение float должно быть < 1. Действительно, дальше мы видим:

Здесь бит маскируется знаковым битом, это используется только для сохранения правильного знака: теперь мы можем полностью игнорировать мантиссу. Мы можем это сделать, потому что в этом случае нас интересует только показатель степени. Так как используется основание степени 2, а e < bias, мы знаем, что наименьший показатель, который может быть, равен -1, а 2 ^ -1 = 0,5. Кроме того, мантисса имеет некоторое значение 1.X. Таким образом, в зависимости от показателя наше число находится либо в диапазоне (0,5, 1), либо в диапазоне (0, 0,5). Поэтому во втором случае для правильного округления нам нужно добавить к числу единицу. Фух. Подробнее это описано в википедии.

Теперь разберём второй случай:

Наверное, вы думаете, что условие в этой ветке должно быть e > bias, чтобы покрыть все случаи с положительным показателем степени. Но вместо этого тут используется только их часть. Использование сдвига здесь особенно интересно, потому что кажется, что оно несравнимо с bias. Первое — это число битов смещения, а второе — численное смещение. Но, поскольку числа с плавающей точкой представлены как (1.мантисса) * 2 ^ X, то если X больше числа битов в мантиссе, мы гарантированно получим значение без дробной части. То есть показатель степени сместил десятичную точку вправо настолько, что мантисса окончательно пропала. Таким образом, выражение в этой ветке игнорирует числа с плавающей точкой, которые уже округлены.

Первая строка тут простая: вычитаем bias из e и получаем реальное значение показателя степени. Вторая строка добавляет к значению 0,5. Это работает, потому что старший бит мантиссы добавляет 0,5 к финальной сумме (см. представление в статье “Википедии” ниже). В этом случае эта сумма переполняет 52-битные границы мантиссы, показатель степени будет увеличен на 1. Значение показателя степени не сможет переполниться до знакового бита, так как оно не может быть больше bias+shift из примера выше. В любом случае, дробная часть очищается. Таким образом, если дробная часть была больше или равна 0,5, она будет увеличена на 1, в противном случае будет отброшена. Хитро и не очевидно до тех пор, пока мы не посмотрим глубже.

Дополнительные функции

Excel содержит и более специфические формулы, использование которых необходимо только в исключительных случаях.

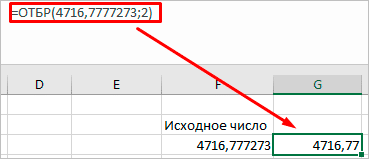
Например, функция ОТБР, которая отбрасывает числа от установленного разряда, то есть происходит не округление, а отсечение.

Функция ОКРВВЕРХ позволяет округлять значение ячейки до целого числа, при этом, если необходимо округлить в большую сторону кратно 100, необходимо указать точность 100, а если до 50, то, соответственно, 50.

Формула ОКРВНИЗ, аналогична предыдущей, только округляется вниз до целого. В зависимости от выбранной точности, можно округлить и до 5, однако это работает только для диапазона значений от 5,00 до 9,99.

Чтобы убрать округление, достаточно удалить из формулы любую из перечисленных функций, при этом исходное значения числа примет первоначальный вид.

Как видите, MS Excel обладает большим набором инструментов для работы с числами. Плюсом является то, что округление можно применять и к суммам, и к результатам вычисления выражений или функций. Описанные выше функции подойдут, как для бухгалтеров и людей, работающих с большими объемами чисел, так и для простых пользователей.

Форматирование чисел

В JavaScript отформатировать вывод числа в соответствии с региональными стандартами (языковыми настройками операционной системы) позволяет метод .

Например, выполним форматирование числа в соответствии с региональными стандартами, которые установлены в системе по умолчанию:

var number = 345.46;
console.log(number.toLocaleString()); //"345,46"

Например, выполним форматирование числа в соответствии с региональными стандартами России (ru):

console.log((108.1).toLocaleString("ru-RU")); //"108,1"

Данный метод можно также использовать для форматирования числа в виде валюты:

console.log((2540.125).toLocaleString("ru-RU",{style:'currency', currency:'RUB'})); //"2 540,13 ₽"
console.log((89.3).toLocaleString("ru-RU",{style:'currency', currency:'USD'})); //"89,30 $"
console.log((2301.99).toLocaleString("ru-RU",{style:'currency', currency:'EUR'})); //"2 301,99 €"

Представление числа в виде процентов:

console.log((0.45).toLocaleString("ru-RU",{style:'percent'})); //"45 %"

Разбить число на разряды (свойство ):

console.log((125452.32).toLocaleString("ru-RU",{useGrouping:true})); //"125 452,32"

Вывести с число с определённым количеством цифр (2) после запятой:

console.log((1240.4564).toLocaleString("ru-RU",{minimumFractionDigits:2, maximumFractionDigits:2})); //"1 240,46"

Relational functions #

Function	Description
math.compare(x, y)	Compare two values.
math.compareNatural(x, y)	Compare two values of any type in a deterministic, natural way.
math.compareText(x, y)	Compare two strings lexically.
math.deepEqual(x, y)	Test element wise whether two matrices are equal.
math.equal(x, y)	Test whether two values are equal.
math.equalText(x, y)	Check equality of two strings.
math.larger(x, y)	Test whether value x is larger than y.
math.largerEq(x, y)	Test whether value x is larger or equal to y.
math.smaller(x, y)	Test whether value x is smaller than y.
math.smallerEq(x, y)	Test whether value x is smaller or equal to y.
math.unequal(x, y)	Test whether two values are unequal.