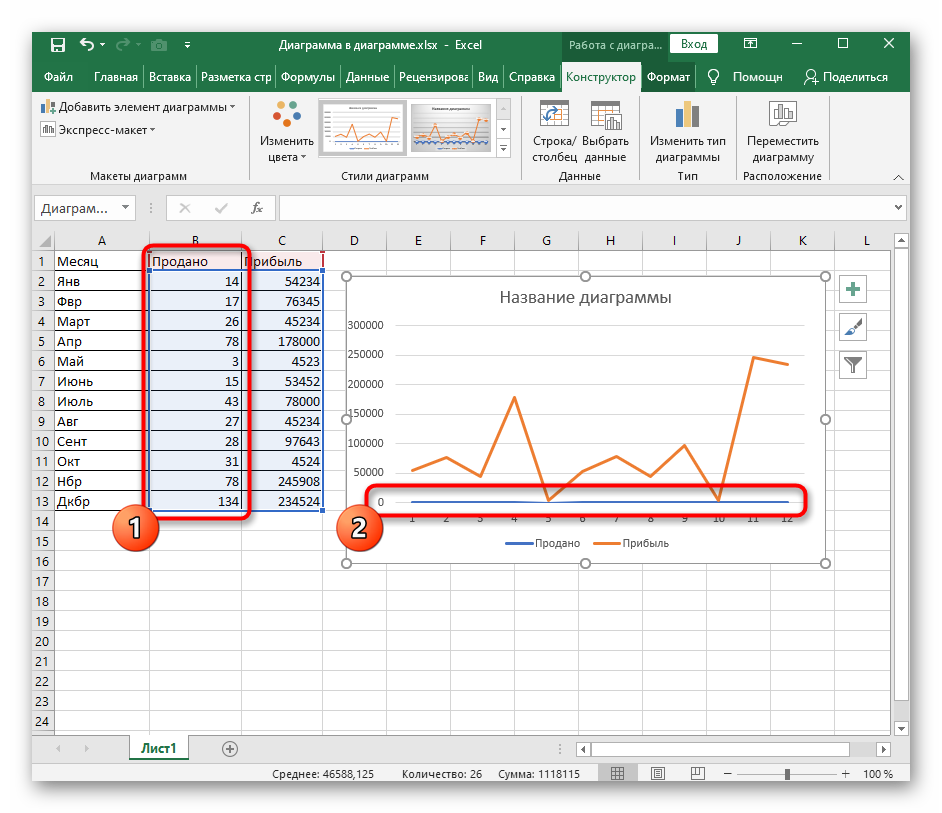
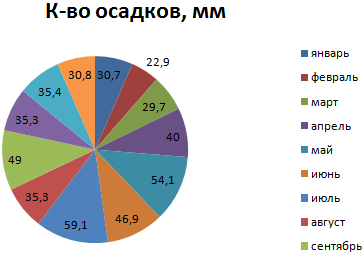
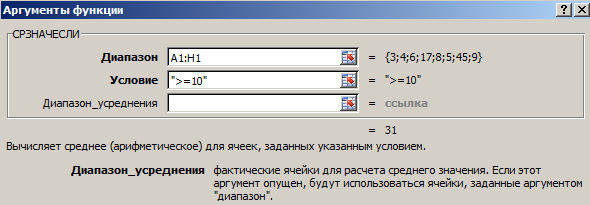
Коэффициент корреляция в excel
Содержание:
Линейный коэффициент корреляции Пирсона
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего.
Это прямая или положительная корреляция.
Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число).
Проверяем значимость коэффициента корреляции (проверяем гипотезу зависимости).
Поскольку оценка коэффициента корреляции вычислена на конечной выборке, и поэтому может отклоняться от своего генерального значения,
необходимо проверить значимость коэффициента корреляции. Проверка производится с помощью t-критерия:
| t = |
|
( 2.1 ) |
Случайная величина t следует t-распределению Стьюдента
и по таблице t-распределения необходимо найти критическое значение критерия (tкр.α) при заданном уровне
значимости α. Если вычисленное по формуле ( 2.1 ) t по модулю окажется меньше
чем tкр.α, то зависимости между случайными величинами X и Y нет. В противном случае, экспериментальные
данные не противоречат гипотезе о зависимости случайных величин.
2.1.t
| t = |
|
= -5.08680 |
2.2.ttкр.αtкр.αα24α0.05tкр.α2.064
Таблица 2 t-распределение
| Число степеней свободы( n — 2 ) | α = 0.1 | α = 0.05 | α = 0.02 | α = 0.01 | α = 0.002 | α = 0.001 |
| 1 | 6.314 | 12.706 | 31.821 | 63.657 | 318.31 | 636.62 |
| 2 | 2.920 | 4.303 | 6.965 | 9.925 | 22.327 | 31.598 |
| 3 | 2.353 | 3.182 | 4.541 | 5.841 | 10.214 | 12.924 |
| 4 | 2.132 | 2.776 | 3.747 | 4.604 | 7.173 | 8.610 |
| 5 | 2.015 | 2.571 | 3.365 | 4.032 | 5.893 | 6.869 |
| 6 | 1.943 | 2.447 | 3.143 | 3.707 | 5.208 | 5.959 |
| 7 | 1.895 | 2.365 | 2.998 | 3.499 | 4.785 | 5.408 |
| 8 | 1.860 | 2.306 | 2.896 | 3.355 | 4.501 | 5.041 |
| 9 | 1.833 | 2.262 | 2.821 | 3.250 | 4.297 | 4.781 |
| 10 | 1.812 | 2.228 | 2.764 | 3.169 | 4.144 | 4.587 |
| 11 | 1.796 | 2.201 | 2.718 | 3.106 | 4.025 | 4.437 |
| 12 | 1.782 | 2.179 | 2.681 | 3.055 | 3.930 | 4.318 |
| 13 | 1.771 | 2.160 | 2.650 | 3.012 | 3.852 | 4.221 |
| 14 | 1.761 | 2.145 | 2.624 | 2.977 | 3.787 | 4.140 |
| 15 | 1.753 | 2.131 | 2.602 | 2.947 | 3.733 | 4.073 |
| 16 | 1.746 | 2.120 | 2.583 | 2.921 | 3.686 | 4.015 |
| 17 | 1.740 | 2.110 | 2.567 | 2.898 | 3.646 | 3.965 |
| 18 | 1.734 | 2.101 | 2.552 | 2.878 | 3.610 | 3.922 |
| 19 | 1.729 | 2.093 | 2.539 | 2.861 | 3.579 | 3.883 |
| 20 | 1.725 | 2.086 | 2.528 | 2.845 | 3.552 | 3.850 |
| 21 | 1.721 | 2.080 | 2.518 | 2.831 | 3.527 | 3.819 |
| 22 | 1.717 | 2.074 | 2.508 | 2.819 | 3.505 | 3.792 |
| 23 | 1.714 | 2.069 | 2.500 | 2.807 | 3.485 | 3.767 |
| 24 | 1.711 | 2.064 | 2.492 | 2.797 | 3.467 | 3.745 |
| 25 | 1.708 | 2.060 | 2.485 | 2.787 | 3.450 | 3.725 |
| 26 | 1.706 | 2.056 | 2.479 | 2.779 | 3.435 | 3.707 |
| 27 | 1.703 | 2.052 | 2.473 | 2.771 | 3.421 | 3.690 |
| 28 | 1.701 | 2.048 | 2.467 | 2.763 | 3.408 | 3.674 |
| 29 | 1.699 | 2.045 | 2.462 | 2.756 | 3.396 | 3.659 |
| 30 | 1.697 | 2.042 | 2.457 | 2.750 | 3.385 | 3.646 |
| 40 | 1.684 | 2.021 | 2.423 | 2.704 | 3.307 | 3.551 |
| 60 | 1.671 | 2.000 | 2.390 | 2.660 | 3.232 | 3.460 |
| 120 | 1.658 | 1.980 | 2.358 | 2.617 | 3.160 | 3.373 |
| ∞ | 1.645 | 1.960 | 2.326 | 2.576 | 3.090 | 3.291 |
2.2.ttкр.αtttкр.αэкспериментальные данные, с вероятностью 0.95αне противоречат гипотезе
Ковариантность прекрасна, но …
Ковариантность — это прекрасный способ количественно оценить движение переменных относительно друг друга, но у него есть некоторые проблемы.
Отличающиеся единицы:Ковариацию трудно интерпретировать, когда единицы двух переменных различны. Например, еслиИксв долларах иYнаходится в фунтах стерлингов единица ковариации междуИкса такжеYстановитсядолларовые времена фунт стерлингов, Как можно это интерпретировать? Даже когда обаИкса такжеYимеют одну и ту же единицу, скажем, доллар, единицы ковариации становится …доллар раз доллар!Все еще не легко понять. Облом!
Отличающиеся весы:Существует также проблема дальности. когдаИкса такжеYварьируются в течение небольшого интервала, скажемвы получите обманчиво крошечное значение ковариации, даже еслиИкса такжеYдвигаться вместе очень плотно.
Сложность со сравнением:Потому чтоИкса такжеYмогут иметь разные единицы измерения и разные диапазоны, зачастую невозможно объективно сравнить ковариацию между одной парой переменных и другой парой переменных. Скажи я хочу сравнитьнасколько сильнее или слабееэто линейная зависимость междуэкономия топлива и длина автомобиляпо сравнению с отношением междуэкономия топлива и снаряженная масса, Использование ковариации для этого сравнения потребует сравнения двух значений в двух разных единицах и двух разных диапазонах. Проблематично, если не сказать больше.
Если бы мы только могли масштабировать ковариацию, чтобы диапазон был стандартизирован, а также решить проблему «единиц» Введите «стандартное отклонение». Проще говоря, стандартное отклонение измеряет среднее отклонение данных от их среднего значения. Стандартное отклонение также имеет приятное свойство: он имеет ту же единицу, что и исходная переменная. Итак, давайте разделим ковариацию на стандартные отклонения двух переменных. Это приведет к изменению масштаба ковариации, так что теперь она выражается вкратные стандартному отклонениюи это будет такжеотмените единицы измерения из числителя, Все неприятности с ковариацией решаются в двух простых делениях! Вот полученная формула:
Где же мы видели эту формулу раньше? Это, конечно, коэффициент корреляции Пирсона!
Литература
- Гмурман В. Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
- Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.
- Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
- Суслов В. И., Ибрагимов Н. М., Талышева Л. П., Цыплаков А. А. Эконометрия. — Новосибирск: СО РАН, 2005. — 744 с. — ISBN 5-7692-0755-8.
Индекс множественной корреляции
 22табл
22табл
4. Оценка значения результативного признака при заданных значениях факторов. Y(0.0,0.0,) = -32.24 + 0.2412 * 0.0 + 0.1151 * 0.0 = -32.24
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака. S2 =
XT(XTX)-1Xгде XT =
(XTX)-1
| 5.8295 | -0.0116 | -0.0002 |
| -0.0116 | 0.0001 | -0 |
| -0.0002 | -0 |
2YY
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
1) t-статистика Статистическая значимость коэффициента регрессии b подтверждается
Статистическая значимость коэффициента регрессии b1 подтверждается Статистическая значимость коэффициента регрессии b2 подтверждается
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими: (bi — t i Si; bi + t i S i) b : (-44.2749;-20.2039)
b 1: (0.204;0.2784) b 2: (0.0887;0.1415)
2) F-статистика. Критерий Фишера Fkp = 4.35 Поскольку F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
6. Проверка на наличие гетероскедастичности методом графического анализа остатков. В этом случае по оси абсцисс откладываются значения объясняющей переменной Xi, а по оси ординат квадраты отклонения ei2.
| y | y(x) | e=y-y(x) | e2 |
| 130.34 | 131.53 | -1.19 | 1.43 |
| 126.83 | 132.94 | -6.11 | 37.35 |
| 108.61 | 105.5 | 3.11 | 9.67 |
| 116.01 | 112.67 | 3.34 | 11.16 |
| 135.44 | 132.68 | 2.76 | 7.63 |
| 142.88 | 149.54 | -6.66 | 44.39 |
| 158.69 | 151.81 | 6.88 | 47.28 |
| 168.49 | 170.91 | -2.42 | 5.87 |
| 174.8 | 178.48 | -3.68 | 13.56 |
| 187.15 | 174.63 | 12.52 | 156.86 |
Как выполняется корреляция в Excel?
«Корреляция» в переводе с латинского обозначает «соотношение», «взаимосвязь». Количественная характеристика взаимосвязи может быть получена при вычислении коэффициента корреляции.
Этот популярный в статистических анализах коэффициент показывает, связаны ли какие-либо параметры друг с другом (например, рост и вес; уровень интеллекта и успеваемость; количество травм и продолжительность работы).
Использование корреляции
Вычисление корреляции особенно широко используется в экономике, социологических исследованиях, медицине и биометрии — везде, где можно получить два массива данных, между которыми может обнаружиться связь.
Рассчитать корреляцию можно вручную, выполняя несложные арифметические действия. Однако процесс вычисления оказывается очень трудоемким, если набор данных велик. Особенность метода в том, что он требует сбора большого количества исходных данных, чтобы наиболее точно отобразить, есть ли связь между признаками.
Поэтому серьезное использование корреляционного анализа невозможно без применения вычислительной техники. Одной из наиболее популярных и доступных программ для решения этой задачи является Microsoft Office Excel.
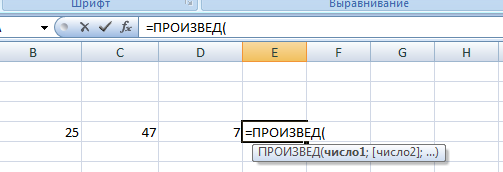
Как выполнить корреляцию в Excel?
Самым трудоемким этапом определения корреляции является набор массива данных. Сравниваемые данные располагаются обычно в двух колонках или строчках. Таблицу следует делать без пропусков в ячейках. Современные версии Excel (с 2007 и младше) не требуют установок дополнительных настроек для статистических расчетов; необходимые манипуляции можно сделать в разделе формул:
- Выбрать пустую ячейку, в которую будет выведен результат расчетов.
- Нажать в главном меню Excel пункт «Формулы».
- Среди кнопок, сгруппированных в «Библиотеку функций», выбрать «Другие функции».
- В выпадающих списках выбрать функцию расчета корреляции (Статистические — КОРРЕЛ).
- В Excel откроется панель «Аргументы функции». «Массив 1» и «Массив 2» — это диапазоны сравниваемых данных. Для автоматического заполнения этих полей можно просто выделить нужные ячейки таблицы.
- Нажать «ОК», закрыв окно аргументов функции. В ячейке появится подсчитанный коэффициент корреляции.
Корреляция может быть прямая (если коэффициент больше нуля) и обратная (от -1 до 0).
Первая означает, что при росте одного параметра растет и другой. Обратная (отрицательная) корреляция отражает факт, что при росте одной переменной другая уменьшается.
Корреляция может быть близка к нулю. Это обычно свидетельствует, что исследуемые параметры не связаны друг с другом. Но иногда нулевая корреляция возникает, если сделана неудачная выборка, которая не отразила связь, либо связь имеет сложный нелинейный характер.
Если коэффициент показывает среднюю или сильную взаимосвязь (от ±0,5 до ±0,99), следует помнить, что это лишь статистическая взаимосвязь, которая вовсе не гарантирует влияние одного параметра на другой. Также нельзя исключать ситуации, что оба параметра независимы друг от друга, но на них воздействует какой-нибудь третий неучтенный фактор.
Excel помогает моментально вычислить коэффициент корреляции, но обычно только количественных методов недостаточно для установления причинно-следственных связей в соотносимых выборках.
Корреляционная функция
Для графического отображения полученных результатов применяют корреляционную функцию (КФ), являющуюся зависимостью коэффициента корреляции явления от временного сдвига (лага). Существует два вида КФ: классическая, или техническая, и интервальная (рис. 7 и рис. 8 соответственно). Классическая корреляционная функция для анализа ЭЭГ не подходит, т.к. при разных t анализу будут подлежать участки разной протяженности, а для сопоставимости коэффициентов корреляции это допустимо только в случае стационарности процессов, которые сохраняют свои свойства на всей протяженности.
Классическая корреляционная функция имеет недостатки:
- невозможность сопоставлять коэффициенты корреляции, которые были вычислены для фрагментов ЭЭГ с различной протяженностью, поскольку полученные коэффициенты будут иметь разные характеристики (т.к. ЭЭГ не является стационарным процессом)
- размер выборки может отличаться; величины на одном конце функции могут быть значимые, а на другом – нет.
Рисунок 7. Классическая, или техническая, корреляционная функция
При построении интервальной корреляционной функции на записи сигнала обращают внимание на корреляционный образец χ длиной Δt, от которого начинается эпоха анализа Т. Чтобы найти связь между явлениями χ при изменении t, необходим анализ равноразмерных участков γ, которые сдвинуты относительно χ на значение τ
(рис. 8)
Если сравнивать интервальную и классическую корреляционные функции, то можно заметить, что интервальная функция имеет несколько преимуществ:
- Используется чаще при выявлении задержек в ЭЭГ-сигнале;
- Повторение этапов высоких значений при сдвигах образца;
- Ее легко интерпретировать.
При исследовании интервальной корреляционной функции необходимо отметить, что высокие значения функции при автокорреляции – это возможное следствие возврата к исходному функциональному состоянию, а в случае кросскорреляционной функции – задержки передачи сигнала между отведениями.
Рисунок 8. Интервальная корреляционная функция
Наиболее чувствительный метод для поиска различий в ЭЭГ-сигналах – огибающая ЭЭГ, оценивающая меру синхронности или асинхронности изменений постсинаптических потенциалов в исследуемых отведениях (амплитуда сигнала повышается при одновременном изменении двух сигналов).
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
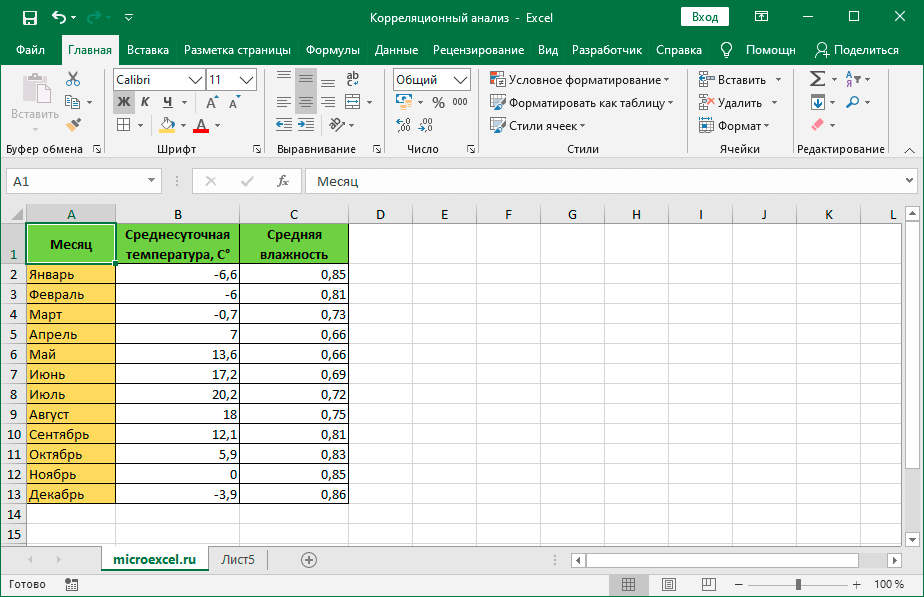
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
Порядок действий при работе с данным инструментом следующий:
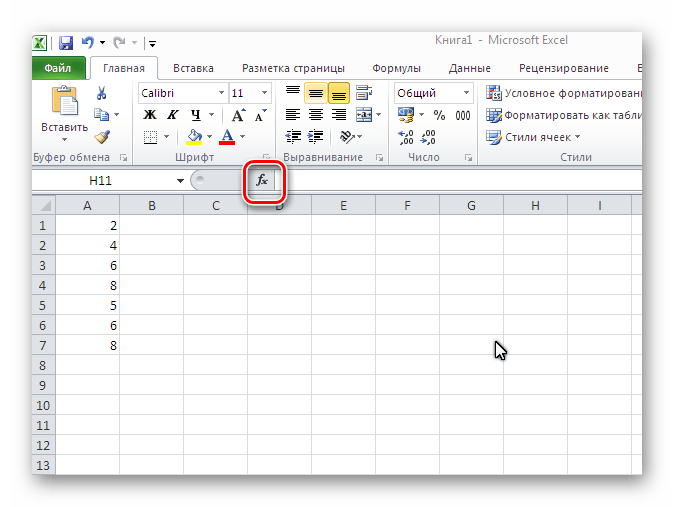
- Встаем в свободную ячейку таблицы, в которой планируем рассчитать коэффициент корреляции. Затем щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- В открывшемся окне вставки функции выбираем категорию “Статистические” (или “Полный алфавитный перечень”), среди предложенных вариантов отмечаем “КОРРЕЛ” и щелкаем OK.
- На экране отобразится окно аргументов функции с установленным курсором в первом поле напротив “Массив 1”. Здесь мы указываем координаты ячеек первого столбца (без шапки таблицы), данные которого требуется проанализировать (в нашем случае – B2:B13). Сделать это можно вручную, напечатав нужные символы с помощью клавиатуры. Также выделить требуемый диапазон можно непосредственно в самой таблице с помощью зажатой левой кнопки мыши. Затем переходим ко второму аргументу “Массив 2”, просто щелкнув внутри соответствующего поля либо нажав клавишу Tab. Здесь указываем координаты диапазона ячеек второго анализируемого столбца (в нашей таблице – это C2:C13). По готовности щелкаем OK.
- Получаем коэффициент корреляции в ячейке с функцией. Значение “-0,63” свидетельствует об умеренно-сильной обратной зависимости между анализируемыми данными.
Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
- Заходим в меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В появившемся окне кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу для параметра “Управление” выбираем “Надстройки Excel” и щелкаем “Перейти”.
- В открывшемся окошке отмечаем “Пакет анализа” и подтверждаем действие нажатием кнопки OK.
Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
- Нажимаем кнопку “Анализ данных”, которая находится во вкладке “Данные”.
- Появится окно, в котором представлен перечень доступных вариантов анализа. Отмечаем “Корреляцию” и щелкаем OK.
- На экране отобразится окно, в котором необходимо указать следующие параметры:
- “Входной интервал”. Выделяем весь диапазон анализируемых ячеек (т.е. сразу оба столбца, а не по одному, как это было в описанном выше методе).
- “Группирование”. На выбор предложено два варианта: по столбцам и строкам. В нашем случае подходит первый вариант, т.к. именно подобным образом расположены анализируемые данные в таблице. Если в выделенный диапазон включены заголовки, следует поставить галочку напротив пункта “Метки в первой строке”.
- “Параметры вывода”. Можно выбрать вариант “Выходной интервал”, в этом случае результаты анализа будут вставлены на текущем листе (потребуется указать адрес ячейки, начиная с которой будут выведены итоги). Также предлагается вывод результатов на новом листе или в новой книге (данные будут вставлены в самом начале, т.е. начиная с ячейки A1). В качестве примера оставляем “Новый рабочий лист” (выбран по умолчанию).
- Когда все готово, щелкаем OK.
- Получаем тот же самый коэффициент корреляции, что и в первом методе. Это говорит о том, что в обоих случаях мы все сделали верно.
Примеры решений онлайн: линейная регрессия
Простая выборка
Пример 1. Имеются данные средней выработки на одного рабочего Y (тыс. руб.) и товарооборота X (тыс. руб.) в 20 магазинах за квартал. На основе указанных данных требуется:
1) определить зависимость (коэффициент корреляции) средней выработки на одного рабочего от товарооборота,
2) составить уравнение прямой регрессии этой зависимости.
Пример 2. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y:
X 100 150 200 250 300
Y 60 35 20 20 15
Найти линейную регрессию Y на X, выборочный коэффициент корреляции.
Пример 3. Найти выборочные числовые характеристики и выборочное уравнение линейной регрессии $y_x=ax+b$. Построить прямую регрессии и изобразить на плоскости точки $(x,y)$ из таблицы. Вычислить остаточную дисперсию. Проверить адекватность линейной регрессионной модели по коэффициенту детерминации.
Пример 4. Вычислить коэффициенты уравнения регрессии. Определить выборочный коэффициент корреляции между плотностью древесины маньчжурского ясеня и его прочностью. Решая задачу необходимо построить поле корреляции, по виду поля определить вид зависимости, написать общий вид уравнения регрессии Y на Х, определить коэффициенты уравнения регрессии и вычислить коэффициенты корреляции между двумя заданными величинами.
Пример 5. Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей X и стоимостью ежемесячного технического обслуживания Y. Для выяснения характера этой связи было отобрано 15 автомобилей. Постройте график исходных данных и определите по нему характер зависимости. Рассчитайте выборочный коэффициент линейной корреляции Пирсона, проверьте его значимость при 0,05. Постройте уравнение регрессии и дайте интерпретацию полученных результатов.
Корреляционная таблица
Пример 6. Найти выборочное уравнение прямой регрессии Y на X по заданной корреляционной таблице
Пример 7. В таблице 2 приведены данные зависимости потребления Y (усл. ед.) от дохода X (усл. ед.) для некоторых домашних хозяйств.
1. В предположении, что между X и Y существует линейная зависимость, найдите точечные оценки коэффициентов линейной регрессии.
2. Найдите стандартное отклонение $s$ и коэффициент детерминации $R^2$.
3. В предположении нормальности случайной составляющей регрессионной модели проверьте гипотезу об отсутствии линейной зависимости между Y и X.
4. Каково ожидаемое потребление домашнего хозяйства с доходом $x_n=7$ усл. ед.? Найдите доверительный интервал для прогноза.
Дайте интерпретацию полученных результатов. Уровень значимости во всех случаях считать равным 0,05.
Решение об исследовании зависимости (4 страницы)
Пример 8. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден.ед.) приводится в таблице:
Необходимо:
1) Вычислить групповые средние и построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
А) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
Б) вычислить коэффициент корреляции, на уровне значимости 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y;
В) используя соответствующее уравнение регрессии, оценить среднюю выручку от мобильных систем с 20 новыми видами тарифов.
Коэффициент корреляции
Пример 9. На основании 18 наблюдений установлено, что на 64% вес X кондитерских изделий зависит от их объема Y. Можно ли на уровне значимости 0,05 утверждать, что между X и Y существует зависимость?
Пример 10. Исследование 27 семей по среднедушевому доходу (Х) и сбережениям (Y) дало результаты: $\overline{X}=82$ у.е., $S_x=31$ у.е., $\overline{Y}=39$ у.е., $S_y=29$ у.е., $\overline{XY} =3709$ (у.е.)2. При $\alpha=0,05$ проверить наличие линейной связи между Х и Y. Определить размер сбережений семей, имеющих среднедушевой доход $Х=130$ у.е.
Нужно решить задачи по на тему регрессия и корреляция?
Оставьте заявку сегодня
Список литературы
- Аблеева, А. М. Формирование фонда оценочных средств в условиях ФГОС / А. М. Аблеева, Г. А. Салимова // Актуальные проблемы преподавания социально-гуманитарных, естественно — научных и технических дисциплин в условиях модернизации высшей школы : материалы международной научно-методической конференции, 4-5 апреля 2014 г. / Башкирский ГАУ, Факультет информационных технологий и управления. — Уфа, 2014. — С. 11-14.
- Ганиева, А.М. Статистический анализ занятости и безработицы / А.М. Ганиева, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 315-316.
- Исмагилов, Р. Р. Творческая группа — эффективная форма организации научных исследований в высшей школе / Р. Р. Исмагилов, М. Х. Уразлин, Д. Р. Исламгулов // Научно-технический и научно-образовательный комплексы региона : проблемы и перспективы развития : материалы научно-практической конференции / Академия наук РБ, УГАТУ. — Уфа, 1999. — С. 105-106.
- Исламгулов, Д.Р. Компетентностный подход в обучении: оценка качества образования / Д.Р. Исламгулов, Т.Н. Лубова, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 62-69.
- Исламгулов, Д. Р. Научно-исследовательская работа студентов — важнейший элемент подготовки специалистов в аграрном вузе / Д. Р. Исламгулов // Проблемы практической подготовки студентов в вузе на современном этапе и пути их решения : сб. материалов науч.-метод. конф., 24 апреля 2007 года / Башкирский ГАУ. — Уфа, 2007. — С. 20-22.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова// БЪДЕЩИТЕ ИЗСЛЕДОВАНИЯ – 2016: Материали за XII Международна научна практична конференция, 15-22 февруари 2016. – София: Бял ГРАД-БГ ООД, 2016. – Том 4 Педагогически науки. – C. 80-85.
- Лубова, Т.Н. Новые образовательные стандарты: особенности реализации / Т.Н. Лубова, Д.Р. Исламгулов // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 79-84.
- Лубова, Т.Н. Организация самостоятельной работы обучающихся / Т.Н. Лубова, Д.Р. Исламгулов // Реализация образовательных программ высшего образования в рамках ФГОС ВО: материалы Всероссийской научно-методической конференции в рамках выездного совещания НМС по природообустройству и водопользованию Федерального УМО в системе ВО. / Башкирский ГАУ. — Уфа, 2016. — С. 214-219.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 85-93.
- Саубанова, Л.М. Уровень демографической нагрузки / Л.М. Саубанова, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 321-322.
- Фахруллина, А.Р. Статистический анализ инфляции в России / А.Р. Фахруллина, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 323-324.
- Фархутдинова, А.Т. Рынок труда в Республике Башкортостан в 2012 году / А.Т. Фархутдинова, Т.Н. Лубова // Студенческий научный форум. Материалы V Международной студенческой электронной научной конференции: электронная научная конференция (электронный сборник). Российская академия естествознания. 2013.